Συναρτησιακή
Δημοσιεύτηκε: Πέμ Ιούλ 22, 2010 6:52 pm
Έστω f : R  R μία συνάρτηση για την οποία ισχύει
R μία συνάρτηση για την οποία ισχύει 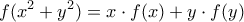 για κάθε
για κάθε  . Να δείξετε ότι
. Να δείξετε ότι
α) f(0) = 0
β) η f είναι περιττή
γ)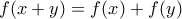 για κάθε
για κάθε 
Είναι άλυτη από φροντιστηριακό βιβλίο .
Ο τρόπος που την έλυσα απαιτεί αλλαγή στο γ) ερώτημα στο .
.
Δείτε την και τα λέμε
 R μία συνάρτηση για την οποία ισχύει
R μία συνάρτηση για την οποία ισχύει 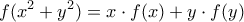 για κάθε
για κάθε  . Να δείξετε ότι
. Να δείξετε ότια) f(0) = 0
β) η f είναι περιττή
γ)
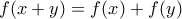 για κάθε
για κάθε 
Είναι άλυτη από φροντιστηριακό βιβλίο .
Ο τρόπος που την έλυσα απαιτεί αλλαγή στο γ) ερώτημα στο
 .
.Δείτε την και τα λέμε
 στην δοσμένη παίρνουμε
στην δοσμένη παίρνουμε 
 στην δοσμένη παίρνουμε
στην δοσμένη παίρνουμε  τότε θέτοντας όπου χ το -χ σ΄ αυτήν εδώ έχω
τότε θέτοντας όπου χ το -χ σ΄ αυτήν εδώ έχω  αφού και οι δυο παραστάσεις είναι ίσες με
αφού και οι δυο παραστάσεις είναι ίσες με  .
. . Για
. Για  σχέση που ισχύει και όταν
σχέση που ισχύει και όταν 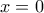 αφού
αφού  η δοσμένη γίνεται
η δοσμένη γίνεται 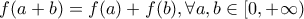 . Αν
. Αν  όμοια και για το b οπότε η αρχικά δοσμένη σχέση ισχύει για τα -a,-b δηλαδή
όμοια και για το b οπότε η αρχικά δοσμένη σχέση ισχύει για τα -a,-b δηλαδή ισχύει για όλα τα x,y του R
ισχύει για όλα τα x,y του R τότε
τότε  για μη αρνητικούς και όμοια για μη θετικούς
για μη αρνητικούς και όμοια για μη θετικούς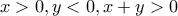 έχουμε
έχουμε  (ομοια και όταν x+y<0)
(ομοια και όταν x+y<0)