Η προσέγγιση του Μίλτου Παπαγρηγοράκη είναι αυτή ακριβώς που είχα στο μυαλό μου.
Θα προσθέσω μερικά πράγματα γύρω από το θέμα για να φανούν οι διασυνδέσεις του με άλλες γνωστές ασκησεις και να έχει ένα χαρακτήρα πληρότητας.
Στα σχολικά βιβλία έχουμε διάφορες ασκήσεις ελαχιστοποίησης απόστασης
(1) Στα Μαθηματικά κατεύθυνσης την "θεωρητική" 200/Β/9
(2) Στα Μαθηματικά κατεύθυνσης την "θεωρητική" 270/Α/5 (η προσέγγιση που έδωσε ο Γιάννης (giannisn1990) είναι στην κατεύθυνση αυτής της άσκησης δηλαδή ελαγιστοποίηση της κατακόρυφης απόστασης)
(
3) Στα Μαθηματικά Γενικής Παιδείας την 45/Α/8
Η
(3) μπορεί εύκολα να τροποποιηθεί και για άλλες συναρτήσεις.
Δύο εύκολες, αλλά όχι χωρίς ενδιαφέρον, που συνηθίζω να κάνω με τους μαθητές μου είναι οι ακόλουθες:
(4) 'Εστω

. Nα βρείτε ποιο σημείο της

απέχει από το σημείο

ελάχιστη απόσταση.
Απάντηση: 
)
(5) Να βρεθεί ποιό σημείο της γραφικής παράστασης της

απέχει από την αρχή των αξόνων ελάχιστη απόσταση.
Απάντηση: Tα σημεία

Επίσης στους μαθητές της κατεύθυνσης διδάσκω,
δίπλα-δίπλα με την
(2) και την:
(6) 'Εστω μία παραγωγίσιμη συνάρτηση

όπου το

είναι ένα ανοικτό διάστημα. 'Eστω

ένα σημείο του επιπέδου. Να αποδείξετε ότι αν ένα σημείο

της

απέχει από το

ελάχιστη απόσταση τότε η εφαπτομένη της

στο

είναι κάθετη στην

.
Απόδειξη: Η άσκηση είναι πολύ γνωστή και λύνεται ως άμεση εφαρμογή του θεωρήματος του Fermat.
Mε αφετηρία την
(6) μπορούμε να αποδείξουμε την πρόταση που αναφέρει ο Μίλτος:
(7) Θεωρούμε

,

(

είναι ένα ανοικτό διάστημα) δύο παραγωγίσιμες συναρτήσεις. Αν

είναι σημεία των

αντιστοίχως και η απόσταση

είναι ελάχιστη τότε το ευθύγραμμο τμήμα

είναι κάθετο στις εφαπτομένες των

στα

,

.
Απόδειξη. Η απόσταση

είναι μικρότερη ή ίση από κάθε απόσταση

με το

να είναι τυχόν σημείο της

. Αρα η

είναι κάθετη στην εφαπτομένη της

στο

. Επαναλαμβάνοντας το επιχείρημα και για το

έχουμε το αποδεικτέο.
Στη συγκεκριμένη τώρα άσκηση ακολουθούμε την διαδικασία που προτείξει ο Μίλτος: Επιχειρηματολογούμε όπως στις
(6),
(7) και καταλήγουμε στο συμπέρασμα ότι oι εφαπτόμενες στα

θα είναι κάθετες στην

και επομένως θα πρέπει να είναι μεταξύ τους παράλληλες.
ΣΗΜΕΙΩΣΗ Φυσικά και πρέπει να προηγηθεί απόδειξη (:το "αποδεικνύεται" που επισημαίνει ο Mίλτος). Σε μία ανάλογη περίπτωση (2005, Μαθηματικά Γενικής Παιδείας, 4ο Θέμα) η επίκληση της διαίσθησης και μόνο δηλαδή χωρίς κάποια απόδειξη στερούσε από τους εξεταζόμενους πολύτιμες μονάδες)
Αν λοιπόν είναι

έχουμε το σύστημα:


Που με λίγη υπομονή δίνουν το ισοδύναμο


και το


'Αρα τα σημεία είναι είναι τα

και

(*)

- leastdist.png (14.82 KiB) Προβλήθηκε 1843 φορές
Μέχρι στιγμής έχουμε άποδείξει ότι
αν η απόσταση AB είναι ελάγιστη τότε τα σημεία πρέπει να είναι τα (*). Για να εξασφαλίσουμε ότι όντως σε αυτά τα σημεία η απόσταση ελαχιστοποιείται χρειάζεται κάποιο είδος επαλήθευσης. Για παράδειγμα να επαληθευθούν οι


ή ισοδύναμα οι


Οι παραγοντοποιήσεις είναι εφικτές γιατί ξέρουμε ότι οι ανισότητες για

,

ισχύουν σαν ισότητες.
Σε γενικές γραμμές η άσκηση
δεν είναι από τις εύκολες. Την συνέθεσα για να καλύφθεί με τους μαθητές μου και αυτή η περίπτωση.
Μαυρογιάννης
 και
και  . Να βρεθούν
. Να βρεθούν 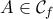 και
και 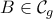 ώστε η απόσταση
ώστε η απόσταση  να είναι ελάχιστη.
να είναι ελάχιστη. και
και  . Να βρεθούν
. Να βρεθούν 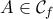 και
και 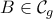 ώστε η απόσταση
ώστε η απόσταση  να είναι ελάχιστη.
να είναι ελάχιστη. και
και 

 ,με την ισότητα να ισχύει για τα σημεία
,με την ισότητα να ισχύει για τα σημεία  και
και 
 . Nα βρείτε ποιο σημείο της
. Nα βρείτε ποιο σημείο της  απέχει από το σημείο
απέχει από το σημείο  ελάχιστη απόσταση.
ελάχιστη απόσταση. )
) απέχει από την αρχή των αξόνων ελάχιστη απόσταση.
απέχει από την αρχή των αξόνων ελάχιστη απόσταση.
 όπου το
όπου το  είναι ένα ανοικτό διάστημα. 'Eστω
είναι ένα ανοικτό διάστημα. 'Eστω  ένα σημείο του επιπέδου. Να αποδείξετε ότι αν ένα σημείο
ένα σημείο του επιπέδου. Να αποδείξετε ότι αν ένα σημείο  της
της  (
(  είναι σημεία των
είναι σημεία των αντιστοίχως και η απόσταση
αντιστοίχως και η απόσταση  με το
με το  να είναι τυχόν σημείο της
να είναι τυχόν σημείο της  . Αρα η
. Αρα η  θα είναι κάθετες στην
θα είναι κάθετες στην  έχουμε το σύστημα:
έχουμε το σύστημα:





 και
και  (*)
(*)




 ,
, ισχύουν σαν ισότητες.
ισχύουν σαν ισότητες. τότε:
τότε: με
με  και
και  δείξτε ότι :
δείξτε ότι :  όπου (ε) είναι η εφαπτομένη της f στο σημείο
όπου (ε) είναι η εφαπτομένη της f στο σημείο 