Σε άσκηση έχουμε δείξει ότι
 .
.Οι παρακάτω ισοδυναμίες χρειάζονται περαιτέρω δικαιολόγηση;
Για
 ισοδύναμα
ισοδύναμα 
Συντονιστής: KAKABASBASILEIOS
 .
. ισοδύναμα
ισοδύναμα 
Μια χαρά είναι.ann79 έγραψε: Σε άσκηση έχουμε δείξει ότι.
Οι παρακάτω ισοδυναμίες χρειάζονται περαιτέρω δικαιολόγηση;
Γιαισοδύναμα
 οπότε υψώνοντας σε δύναμη
οπότε υψώνοντας σε δύναμη  έπεται..."
έπεται..."Καλύτερα θα ήταν έτσι :ann79 έγραψε:Καλημέρα.
Σε άσκηση έχουμε δείξει ότι.
Οι παρακάτω ισοδυναμίες χρειάζονται περαιτέρω δικαιολόγηση;
Γιαισοδύναμα
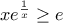 και εφόσον η συνάρτηση
και εφόσον η συνάρτηση  , με
, με  είναι γνησίως αύξουσα, θα είναι :
είναι γνησίως αύξουσα, θα είναι : , για
, για 
Νομίζω θέλειΛάμπρος Μπαλός έγραψε: ↑Τετ Απρ 20, 2016 11:03 amΚαλύτερα θα ήταν έτσι :ann79 έγραψε:Καλημέρα.
Σε άσκηση έχουμε δείξει ότι.
Οι παρακάτω ισοδυναμίες χρειάζονται περαιτέρω δικαιολόγηση;
Γιαισοδύναμα
και εφόσον η συνάρτηση
, με
είναι γνησίως αύξουσα, θα είναι :
, για
Αλλά και έτσι που το έχεις μια χαρά είναι, ας μη βγάζουμε κι από τη μύγα ξίγκι.
 χωρίς να θέλω να γίνω pedant...
χωρίς να θέλω να γίνω pedant... Ενδιαφέρον λίαν!Mihalis_Lambrou έγραψε: ↑Τετ Απρ 20, 2016 10:59 am...
Η απαίτηση για προσθήκη θα ήταν περίπτωση που στα αγγλικά ονομάζεται pedantic (*).
Αν αναλωνόμαστε σε τέτοιες συζητήσεις, χάνουμε την ουσία των Μαθηματικών. Τα Μαθηματικά είναι αλλού, όχι σε ανησυχία για το παραπάνω.
(*) Από λεξικό: Pedant. One who is interested in words and rules rather than making wise use of knowledge (Κάποιος που ενδιαφέρεται περισσότερο για λόγια και κανόνες αντί να κάνει σοφή χρήση της γνώσης).
 είναι κυρτή στο
είναι κυρτή στο  αφού:
αφού:
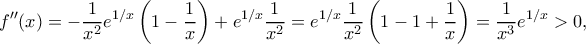
 .
. στο
στο  είναι η:
είναι η:
 είναι κυρτή η γραφική της παράσταση θα βρίσκεται πάνω από την εφαπτομένη της, οπότε:
είναι κυρτή η γραφική της παράσταση θα βρίσκεται πάνω από την εφαπτομένη της, οπότε:

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες