
για κάθε

καθώς και

Να βρεθεί ο τύπος της f.
Ευχαριστώ εκ των προτέρων
Συντονιστής: KAKABASBASILEIOS



Για να την προσπαθήσεις σου δίδω υπόδειξη:
 δε μπορεί να έχει θετικό μέγιστο στο τυχόν
δε μπορεί να έχει θετικό μέγιστο στο τυχόν  αλλά και ούτε αρνητικό ελάχιστο. Συμπέρανε ότι η
αλλά και ούτε αρνητικό ελάχιστο. Συμπέρανε ότι η  είναι η μηδενική συνάρτηση.
είναι η μηδενική συνάρτηση.
Αν ηTolaso J Kos έγραψε: ↑Τρί Ιαν 23, 2018 9:45 amΓια να την προσπαθήσεις σου δίδω υπόδειξη:
Δείξε ότι ηδε μπορεί να έχει θετικό μέγιστο στο τυχόν
αλλά και ούτε αρνητικό ελάχιστο. Συμπέρανε ότι η
είναι η μηδενική συνάρτηση.
Προσθήκη αρκετή ώρα αργότερα:
 είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο  και γνησίως αύξουσα στο
και γνησίως αύξουσα στο ![(-\infty ,0] (-\infty ,0]](/forum/ext/geomar/texintegr/latexrender/pictures/f9d75a40b8eadac31117745d2255ef61.png)
 .
.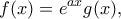 όπου το
όπου το  θα το διαλέξουμε αργότερα. Φυσικά είναι
θα το διαλέξουμε αργότερα. Φυσικά είναι 
 , οπότε η συνθήκη γράφεται
, οπότε η συνθήκη γράφεται
 μια ρίζα της εξίσωσης
μια ρίζα της εξίσωσης  η συνθήκη γίνεται
η συνθήκη γίνεται (λόγω των
(λόγω των 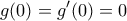 ),
),  είναι σταθερή, οπότε μηδενική. Επομένως είναι
είναι σταθερή, οπότε μηδενική. Επομένως είναι 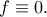
.
 ρίζα της
ρίζα της  , η εξίσωση γράφεται
, η εξίσωση γράφεται  (που είναι της μορφής
(που είναι της μορφής  ).
).  , που από τις
, που από τις  δίνει
δίνει  . Άρα
. Άρα  , οπότε
, οπότε  , που από την
, που από την  δίνει
δίνει  . Τελικά,
. Τελικά,  .
. (1) όταν
(1) όταν 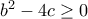
 τότε η εξίσωση
τότε η εξίσωση  έχει δυο ρίζες
έχει δυο ρίζες  και
και  με
με  και
και  οπότε η (1) γίνεται
οπότε η (1) γίνεται οπότε
οπότε και
και 
 τα πράγματα είναι πιο εύκολα διότι έχουμε μια ρίζα
τα πράγματα είναι πιο εύκολα διότι έχουμε μια ρίζα  και η (1) γίνεται
και η (1) γίνεται 


Χάνω κάτι;Παπαστεργίου Κώστας έγραψε: ↑Τετ Φεβ 07, 2018 1:02 amη παραλλαγή του κ Λάμπρου φαντάζει ασύλληπτη στο νου ενός μαθητή. Επιτρέψτε μου να δώσω μια δική μου που πιστεύω ότι είναι πιο κατανοητή και σίγουρα γενικότερη.
 είναι ειδικοί αριθμοί, όπως δίνονται, και όχι η προφανής γενίκευση. Ας προσθέσω ότι οι τεχνικές αυτές είναι στάνταρ, χιλιοειπωμένες, που υπάρχουν στην μία ή την άλλη μορφή σε όλα τα βιβλία Διαφορικών Εξισώσεων.
είναι ειδικοί αριθμοί, όπως δίνονται, και όχι η προφανής γενίκευση. Ας προσθέσω ότι οι τεχνικές αυτές είναι στάνταρ, χιλιοειπωμένες, που υπάρχουν στην μία ή την άλλη μορφή σε όλα τα βιβλία Διαφορικών Εξισώσεων.Αμ δεν είναι το ίδιο. Αναφέρεσαι μόνο στηνMihalis_Lambrou έγραψε: ↑Τετ Φεβ 07, 2018 8:44 amΧάνω κάτι;Παπαστεργίου Κώστας έγραψε: ↑Τετ Φεβ 07, 2018 1:02 amη παραλλαγή του κ Λάμπρου φαντάζει ασύλληπτη στο νου ενός μαθητή. Επιτρέψτε μου να δώσω μια δική μου που πιστεύω ότι είναι πιο κατανοητή και σίγουρα γενικότερη.
Αυτό που έκανα είναι ακριβώς το ίδιο με αυτό που γράφεις. Μάλιστα κατά τι ευκολότερο γιατί ταείναι ειδικοί αριθμοί, όπως δίνονται, και όχι η προφανής γενίκευση. Ας προσθέσω ότι οι τεχνικές αυτές είναι στάνταρ, χιλιοειπωμένες, που υπάρχουν στην μία ή την άλλη μορφή σε όλα τα βιβλία Διαφορικών Εξισώσεων.
 όπου παρουσιάζεις, ως από μηχανής θεό, τη ρίζα της
όπου παρουσιάζεις, ως από μηχανής θεό, τη ρίζα της  , δεν εξηγείς γιατί αυτή και όχι την
, δεν εξηγείς γιατί αυτή και όχι την  ούτε πως έφτασες στην
ούτε πως έφτασες στην  . Σε μαθητές απευθύνεσαι.
. Σε μαθητές απευθύνεσαι.Καλύτερα να μένουμε μόνο στα επιστημονικά θέματα και στο επίπεδο που έχει καθιερωθεί στο φόρουμ.Παπαστεργίου Κώστας έγραψε: ↑Πέμ Φεβ 08, 2018 12:38 pmΜε ρωτάς αν χάνεις κάτι. Την ψυχραιμία σου σίγουρα. Για κάτι άλλο ψάξτο μόνος σου. Σου χαρίζω τον τελευταίο λόγο.
είναι λιγότερο ουρανοκατέβατο από το
Το αφήνω στην κρίση των αναγνωστών.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες