 θετικοί ακέραιοι με
θετικοί ακέραιοι με  , υπολογίστε το άθροισμα:
, υπολογίστε το άθροισμα: 
To
 παριστάνει τους συνδυασμούς των
παριστάνει τους συνδυασμούς των  ανά
ανά  .
.Συντονιστής: KAKABASBASILEIOS
 θετικοί ακέραιοι με
θετικοί ακέραιοι με  , υπολογίστε το άθροισμα:
, υπολογίστε το άθροισμα: 
 παριστάνει τους συνδυασμούς των
παριστάνει τους συνδυασμούς των  ανά
ανά  .
.Καλησπέρα κ.Λουρίδα και καλή ανάσταση να έχετε.Το αποτέλεσμα είναιS.E.Louridas έγραψε: ↑Παρ Απρ 06, 2018 6:41 pmΑνθετικοί ακέραιοι με
, υπολογίστε το άθροισμα:

Toπαριστάνει τους συνδυασμούς των
ανά
.
 και το ίδιο ισχύει αν αντί του
και το ίδιο ισχύει αν αντί του  έχουμε οποιοδήποτε πολυώνυμο
έχουμε οποιοδήποτε πολυώνυμο  βαθμού το
βαθμού το 
 Από το διωνυμικό θεώρημα και με τη σύμβαση
Από το διωνυμικό θεώρημα και με τη σύμβαση 

 όπου
όπου 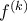 η
η  οστή παράγωγος και
οστή παράγωγος και 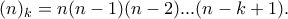
 παραγωγίζοντας
παραγωγίζοντας  φορές παίρνουμε
φορές παίρνουμε  Επομένως
Επομένως 
 όπου
όπου  το
το  παίρνουμε
παίρνουμε 


 είναι πλήρως καθορισμένη από τις τιμές του
είναι πλήρως καθορισμένη από τις τιμές του 
 αφού
αφού 
 αντικαθιστώντας στη
αντικαθιστώντας στη  όπου
όπου  το
το  βρίσκουμε ότι το άθροισμά μας έχει τιμή
βρίσκουμε ότι το άθροισμά μας έχει τιμή  (είναι επίσης
(είναι επίσης 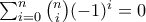 ) και εμπροσθοδρομικά
) και εμπροσθοδρομικά  είναι
είναι 
Ευχαριστώ πολύ, Καλή Ανάσταση και σε σας.Λάμπρος Κατσάπας έγραψε: ↑Σάβ Απρ 07, 2018 8:34 pmΚαλησπέρα κ.Λουρίδα και καλή ανάσταση να έχετε.Το αποτέλεσμα είναιS.E.Louridas έγραψε: ↑Παρ Απρ 06, 2018 6:41 pmΑνθετικοί ακέραιοι με
, υπολογίστε το άθροισμα:

Toπαριστάνει τους συνδυασμούς των
ανά
.
και το ίδιο ισχύει αν αντί του
έχουμε οποιοδήποτε πολυώνυμο
βαθμού το
πολύ
Θεωρούμε τη συνάρτησηΑπό το διωνυμικό θεώρημα και με τη σύμβαση
είναι
Επίσης,όπου
η
οστή παράγωγος και
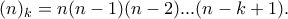
Από τηνπαραγωγίζοντας
φορές παίρνουμε
Επομένως
Αν θέσουμε στηόπου
το
παίρνουμε


για κάποιες πραγματικές σταθερές
Από την τελευταία βλέπουμε ότι η τιμή του αθροίσματοςείναι πλήρως καθορισμένη από τις τιμές του

γιααφού
Γιααντικαθιστώντας στη
όπου
το
βρίσκουμε ότι το άθροισμά μας έχει τιμή
και εμπροσθοδρομικά καταλήγουμε ότι για κάθε
είναι

Βιαστικά γιατί είμαι στο εξωτερικό (όμως δεν θα χάσω το Πασχαλινό αρνί σήμερα μια και αργότερα θα συναντηθώ με την ελληνική κοινότητα εδώ)S.E.Louridas έγραψε: ↑Παρ Απρ 06, 2018 6:41 pmΑνθετικοί ακέραιοι με
, υπολογίστε το άθροισμα:

Toπαριστάνει τους συνδυασμούς των
ανά
.

 παίρνουμε ότι για
παίρνουμε ότι για  το δοθέν άθροισμα ισούται με
το δοθέν άθροισμα ισούται με  .
. 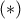 έχουμε
έχουμε 
 παίρνουμε ότι για
παίρνουμε ότι για  το δοθέν άθροισμα επίσης ισούται με
το δοθέν άθροισμα επίσης ισούται με  . Θα δούμε ότι συμβαίνει το ίδιο για τα υπόλοιπα
. Θα δούμε ότι συμβαίνει το ίδιο για τα υπόλοιπα  μέχρι το
μέχρι το  .
.  επί
επί  έχουμε
έχουμε 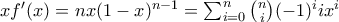 . Παραγωγίζοντας και μετά θέτοντας
. Παραγωγίζοντας και μετά θέτοντας  παίρνουμε ότι για
παίρνουμε ότι για  το δοθέν άθροισμα επίσης ισούται με
το δοθέν άθροισμα επίσης ισούται με  .
. , παραγωγίζουμε και θέτουμε
, παραγωγίζουμε και θέτουμε  . Το άθροισμα τα βγει
. Το άθροισμα τα βγει  λόγω της ύπαρξης παράγοντα
λόγω της ύπαρξης παράγοντα  στο αριστερό μέλος. Και λοιπά.
στο αριστερό μέλος. Και λοιπά. .
.Για να είμαι ειλικρινής Δημήτρη, απλά θεώρησα ότι με "άνοιγμα" του αθροίσματος, ώστε να έχουμε πιο προσιτή προσέγγιση και θεωρώντας τον
 ως σταθερό και σε κάθε φυσικό αριθμό
ως σταθερό και σε κάθε φυσικό αριθμό  τέτοιον ώστε
τέτοιον ώστε  να αντιστοιχούμε πολυώνυμο
να αντιστοιχούμε πολυώνυμο  καταλήγουμε σε ύλη της 3ης Λυκείου, κύρια με σειρά παραγωγίσεων (Ο διδακτικός μου στόχος ήταν και αυτός, δηλαδή να μην μένει ο λύτης σε κάποιες περιπτώσεις μόνο σε μία ή δύο παραγωγίσεις, αλλά να έχει στο μυαλό του ότι πιθανόν να χρειαστούν πάνω από το συνηθισμένο πλήθος παραγωγίσεων). Όμως τώρα που το ξανασκέφτομαι με την δική σου επισήμανση θα μπορούσε να πάει στον φάκελο «Ανάλυση».
καταλήγουμε σε ύλη της 3ης Λυκείου, κύρια με σειρά παραγωγίσεων (Ο διδακτικός μου στόχος ήταν και αυτός, δηλαδή να μην μένει ο λύτης σε κάποιες περιπτώσεις μόνο σε μία ή δύο παραγωγίσεις, αλλά να έχει στο μυαλό του ότι πιθανόν να χρειαστούν πάνω από το συνηθισμένο πλήθος παραγωγίσεων). Όμως τώρα που το ξανασκέφτομαι με την δική σου επισήμανση θα μπορούσε να πάει στον φάκελο «Ανάλυση». Θεωρούμε τον
Θεωρούμε τον  ως σταθερά και σε κάθε
ως σταθερά και σε κάθε  αντιστοιχούμε το πολυώνυμο
αντιστοιχούμε το πολυώνυμο  οπότε
οπότε  Παρατηρούμε εύκολα ότι
Παρατηρούμε εύκολα ότι  και βέβαια
και βέβαια 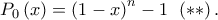 Από τις σχέσεις
Από τις σχέσεις  παίρνουμε επαγωγικά τα πολυώνυμα
παίρνουμε επαγωγικά τα πολυώνυμα  με
με  κάποιο πολυώνυμο. Για
κάποιο πολυώνυμο. Για  έχουμε
έχουμε  Τελικά παίρνουμε
Τελικά παίρνουμε 
 . Αφού
. Αφού  μπορούμε να ξεκινήσουμε την άθροιση από το
μπορούμε να ξεκινήσουμε την άθροιση από το  .
.
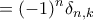 (όπου
(όπου  το δέλτα του Kronecker).
το δέλτα του Kronecker). (αποδεικνύεται με επαγωγή στο
(αποδεικνύεται με επαγωγή στο  ). Επομένως,
). Επομένως,  .
.Χρόνια πολλά κ.Δημήτρη (και στον κ.Σκουτέρη και κ. Λάμπρου βεβαίως)
 και
και  , για
, για  παίρνουμε
παίρνουμε 
 για
για  ενώ για
ενώ για  έχουμε
έχουμε 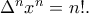
 και
και  έχουμε από την
έχουμε από την  ότι
ότι 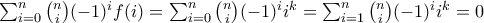
 και
και  είναι
είναι 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες