exdx έγραψε: ↑Σάβ Ιούλ 14, 2018 10:40 pm
Δίνονται οι συναρτήσεις :

και

και τα σημεία
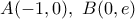
.
α) Να αποδείξετε ότι η εξίσωση

έχει ακριβώς δύο πραγματικές ρίζες , έστω

με

β) Η συνάρτηση
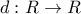
παριστάνει την απόσταση ενός τυχαίου σημείου

της

από την ευθεία

.
i) Να βρείτε τον τύπο της συνάρτησης

ii) Να τη μελετήσετε ως προς τη μονοτονία και τα ακρότατα .
...γεια σου Γιώργη καλησπέρα

με μια προσπάθεια στο θέμα...
α) Είναι

είναι συνεχής στο

με

και
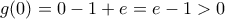
και

άρα είναι

και σύμφωνα με το θεώρημα του Bolzano υπάρχουν

που
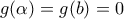
Αν τώρα η

έχει τρεις διαφορετικές ρίζες

επειδή η

είναι παραγωγίσιμη με

σύμφωνα με το θεώρημα του Rolle στα
![[{{\rho }_{1}},\,{{\rho }_{2}}],\,\,[{{\rho }_{2}},\,{{\rho }_{3}}] [{{\rho }_{1}},\,{{\rho }_{2}}],\,\,[{{\rho }_{2}},\,{{\rho }_{3}}]](/forum/ext/geomar/texintegr/latexrender/pictures/e8ee2b147a2d7ff37ed884fdebf32cae.png)
υπάρχουν

που
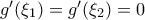
που είναι άτοπο γιατί
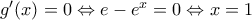
επομένως η

έχει ακριβώς δύο πραγματικές ρίζες , τις

με

β) i) Η ευθεία

έχει εξίσωση
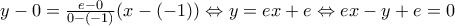
και
η απόσταση του τυχαίου σημείου

από αυτή είναι

ii) Σύμφωνα με το (α)

είναι οι μοναδικές ρίζες της

(και της

και λόγω αυτού

άρα σαν συνεχής θα έχει σταθερό πρόσημο σε κάθε διάστημα , έτσι αφού

και

είναι

και

με
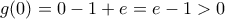
άρα

και τέλος

και
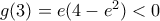
άρα

έτσι έχουμε

που είναι παραγωγίσιμη για

με

ή

και αφού

και έχουμε ότι
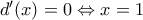
είναι

άρα η

είναι γνήσια φθίνουσα στα
![x\in (-\infty ,\,\alpha ],\,\,[1,\,b] x\in (-\infty ,\,\alpha ],\,\,[1,\,b]](/forum/ext/geomar/texintegr/latexrender/pictures/f7b8bfc43755229a32b4560398962ec1.png)
και ακόμη είναι

άρα η

είναι γνήσια αύξουσα στα
![[\alpha ,\,\,1],\,\,[b,\,\,+\infty ) [\alpha ,\,\,1],\,\,[b,\,\,+\infty )](/forum/ext/geomar/texintegr/latexrender/pictures/bae56d86feb30a77223646f312d75b10.png)
οπότε παρουσιάζει ελάχιστο στα

το
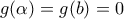
Φιλικά και Μαθηματικά
Βασίλης
 και
και  και τα σημεία
και τα σημεία 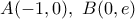 .
. έχει ακριβώς δύο πραγματικές ρίζες , έστω
έχει ακριβώς δύο πραγματικές ρίζες , έστω  με
με 
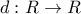 παριστάνει την απόσταση ενός τυχαίου σημείου
παριστάνει την απόσταση ενός τυχαίου σημείου  της
της  από την ευθεία
από την ευθεία  .
.

 με
με  και
και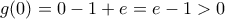 και
και 

 που
που 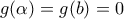
 επειδή η
επειδή η  είναι παραγωγίσιμη με
είναι παραγωγίσιμη με  σύμφωνα με το θεώρημα του Rolle στα
σύμφωνα με το θεώρημα του Rolle στα ![[{{\rho }_{1}},\,{{\rho }_{2}}],\,\,[{{\rho }_{2}},\,{{\rho }_{3}}] [{{\rho }_{1}},\,{{\rho }_{2}}],\,\,[{{\rho }_{2}},\,{{\rho }_{3}}]](/forum/ext/geomar/texintegr/latexrender/pictures/e8ee2b147a2d7ff37ed884fdebf32cae.png)
 που
που 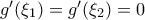 που είναι άτοπο γιατί
που είναι άτοπο γιατί 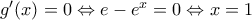 επομένως η
επομένως η 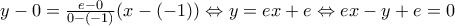 και
και  από αυτή είναι
από αυτή είναι 
 και λόγω αυτού
και λόγω αυτού  άρα σαν συνεχής θα έχει σταθερό πρόσημο σε κάθε διάστημα , έτσι αφού
άρα σαν συνεχής θα έχει σταθερό πρόσημο σε κάθε διάστημα , έτσι αφού  και
και  και
και  με
με  και τέλος
και τέλος  και
και 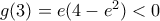 άρα
άρα  έτσι έχουμε
έτσι έχουμε  που είναι παραγωγίσιμη για
που είναι παραγωγίσιμη για  με
με  ή
ή 
 και έχουμε ότι
και έχουμε ότι 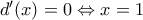 είναι
είναι 
 είναι γνήσια φθίνουσα στα
είναι γνήσια φθίνουσα στα ![x\in (-\infty ,\,\alpha ],\,\,[1,\,b] x\in (-\infty ,\,\alpha ],\,\,[1,\,b]](/forum/ext/geomar/texintegr/latexrender/pictures/f7b8bfc43755229a32b4560398962ec1.png) και ακόμη είναι
και ακόμη είναι  άρα η
άρα η ![[\alpha ,\,\,1],\,\,[b,\,\,+\infty ) [\alpha ,\,\,1],\,\,[b,\,\,+\infty )](/forum/ext/geomar/texintegr/latexrender/pictures/bae56d86feb30a77223646f312d75b10.png)
 το
το