exdx έγραψε: ↑Πέμ Αύγ 09, 2018 7:50 pm
Δίνεται ο αριθμός
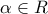
και η συνάρτηση

,

.
Δ1. Να αποδείξετε ότι για κάθε τιμή του

η γραφική παράσταση της συνάρτησης

έχει ακριβώς ένα σημείο καμπής και να βρείτε την εξίσωση της γραμμής

στην οποία ανήκει .
Δ2. Να βρείτε για ποιες τιμές του

υπάρχουν μοναδικά

με

, τέτοια ώστε η συνάρτηση

να παρουσιάζει τοπικό μέγιστο στο
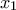
και τοπικό ελάχιστο στο

.
Δ3. α) Να βρείτε την εξίσωση της γραμμής

στην οποία ανήκουν τα σημεία

β) Να βρείτε σε ποιο τμήμα της

ανήκει το

και σε ποιο το

.
Δ4. Να βρείτε το πλήθος των ριζών της εξίσωσης

όταν το

διατρέχει το

.
1. Είναι

Λύνοντας την εξίσωση

βρίσκουμε λύση την

. Για

είναι

ενώ για

είναι

. Από τα τελευταία παίρνουμε ότι το

είναι σημείο καμπής.
Για

βρίσκουμε

που είναι η ζητούμενη εξίσωση της
 2.
2. Πρέπει η

να έχει δύο ακριβώς λύσεις. Επειδή το αριστερό μέλος είναι θετικό
θα αναζητήσουμε λύσεις στο

Για

από την γνωστή

έχουμε

δηλαδή έχουμε αδύνατη εξίσωση. Για

έχουμε

με την ισότητα μόνο για

(άρα μία μόνο ρίζα).Βλέπουμε λοιπόν ότι η αν η

έχει δύο ακριβώς ρίζες τότε

.
Θα δείξουμε ότι ισχύει και το αντίστροφο. Πράγματι για

έχουμε

αλλά

γιατί η
τελευταία είναι ισοδύναμη με την

Άρα


Επίσης
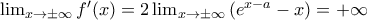

.
Συνδυάζοντας τα

και χρησιμοποιώντας το Θ.BOLZANO βλέπουμε (λόγω συνέχειας της

) ότι η

έχει
τουλάχιστον δύο ρίζες όταν

. Τρεις όμως δεν μπορεί να έχει γιατί από Θ.ROLLE θα είχαμε ότι η

έχει τουλάχιστον δύο ρίζες (άτοπο από
1). Εναλλακτικά από τη μονοτονία
της

(από το
1 ξέρουμε την

) στα διαστήματα

και τη

πάλι καταλήγουμε στο γεγονός ότι η

έχει ακριβώς δύο ρίζες, μια στο

και μια
στο
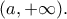
Άρα αν

τότε η

έχει δύο ακριβώς ρίζες τις οποίες ας τις πούμε

με

Εύκολα βλέπουμε ότι από τη συνέχεια της

και από τις

ότι

για κάθε

και

για κάθε

Επομένως το
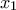
είναι θέση τοπικού
μεγίστου και το

είναι θέση τοπικού ελαχίστου.
Συνέχεια...
3.α Τα

προέκυψαν από τη λύση της

Επομένως,

δηλαδή

και

Είναι φανερό τώρα ότι η

έχει εξίσωση

.
3.β Έχουμε ήδη αποδείξει ότι

Επομένως το

βρίσκεται στο τμήμα της

ανάμεσα στις κατακόρυφες ευθείες
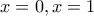
ενώ το

στο τμήμα της

δεξιά της
κατακόρυφης ευθείας
 4.
4. Θεωρούμε την

για την οποία ισχύει
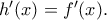
Για

έχουμε δείξει στο
2 ότι

οπότε η

είναι
γνησίως αύξουσα. Είναι όμως


και επομένως από τη συνέχεια, τη μονοτονία της

και το γεγονός ότι

(από

)
παίρνουμε μια μόνο ρίζα της

. Στο ίδιο συμπέρασμα καταλήγουμε αν υποθέσουμε ότι

αφού τότε
θα είναι

με ισότητα μόνο για

Πάμε για

Για σταθερό

η

και η

έχουν τις ίδιες θέσεις τοπικού μεγίστου και ελαχίστου

αφού διαφέρουν κατά τη σταθερά

(έχουν ίδια παράγωγο άρα οι εξισώσεις
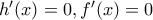
έχουν ίδιες ρίζες κ.λ.π.). Δείχνουμε τώρα ότι για

είναι

και
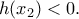
Από
την

και ο γεγονός ότι η

είναι γνησίως φθίνουσα στο

παίρνουμε
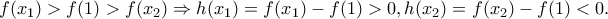
Το τελευταίο αποτέλεσμα σε
συνδυασμό με την

τη συνέχεια της

και τη μονοτονία της (που είναι ίδια με τη μονοτονία της

λόγω κοινής παραγώγου) μας δίνει τελικά ότι η

έχει τρεις ρίζες για

οι οποίες
βρίσκονται συγκεκριμένα στα διαστήματα

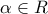 και η συνάρτηση
και η συνάρτηση  ,
,  .
. η γραφική παράσταση της συνάρτησης
η γραφική παράσταση της συνάρτησης  έχει ακριβώς ένα σημείο καμπής και να βρείτε την εξίσωση της γραμμής
έχει ακριβώς ένα σημείο καμπής και να βρείτε την εξίσωση της γραμμής  στην οποία ανήκει .
στην οποία ανήκει . υπάρχουν μοναδικά
υπάρχουν μοναδικά  με
με  , τέτοια ώστε η συνάρτηση
, τέτοια ώστε η συνάρτηση  να παρουσιάζει τοπικό μέγιστο στο
να παρουσιάζει τοπικό μέγιστο στο 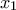 και τοπικό ελάχιστο στο
και τοπικό ελάχιστο στο  .
.  στην οποία ανήκουν τα σημεία
στην οποία ανήκουν τα σημεία 
 ανήκει το
ανήκει το  και σε ποιο το
και σε ποιο το  .
. όταν το
όταν το  διατρέχει το
διατρέχει το  .
.
 Λύνοντας την εξίσωση
Λύνοντας την εξίσωση  βρίσκουμε λύση την
βρίσκουμε λύση την  . Για
. Για  είναι
είναι  ενώ για
ενώ για  είναι
είναι  . Από τα τελευταία παίρνουμε ότι το
. Από τα τελευταία παίρνουμε ότι το  είναι σημείο καμπής.
είναι σημείο καμπής.  βρίσκουμε
βρίσκουμε  που είναι η ζητούμενη εξίσωση της
που είναι η ζητούμενη εξίσωση της 
 να έχει δύο ακριβώς λύσεις. Επειδή το αριστερό μέλος είναι θετικό
να έχει δύο ακριβώς λύσεις. Επειδή το αριστερό μέλος είναι θετικό  Για
Για  από την γνωστή
από την γνωστή  έχουμε
έχουμε  δηλαδή έχουμε αδύνατη εξίσωση. Για
δηλαδή έχουμε αδύνατη εξίσωση. Για  έχουμε
έχουμε 
 (άρα μία μόνο ρίζα).Βλέπουμε λοιπόν ότι η αν η
(άρα μία μόνο ρίζα).Βλέπουμε λοιπόν ότι η αν η  έχει δύο ακριβώς ρίζες τότε
έχει δύο ακριβώς ρίζες τότε  .
.  αλλά
αλλά  γιατί η
γιατί η  Άρα
Άρα 
 Επίσης
Επίσης 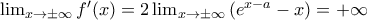
 .
.  και χρησιμοποιώντας το Θ.BOLZANO βλέπουμε (λόγω συνέχειας της
και χρησιμοποιώντας το Θ.BOLZANO βλέπουμε (λόγω συνέχειας της  ) ότι η
) ότι η  έχει τουλάχιστον δύο ρίζες (άτοπο από 1). Εναλλακτικά από τη μονοτονία
έχει τουλάχιστον δύο ρίζες (άτοπο από 1). Εναλλακτικά από τη μονοτονία  (από το 1 ξέρουμε την
(από το 1 ξέρουμε την  ) στα διαστήματα
) στα διαστήματα  και τη
και τη  και μια
και μια 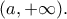 Άρα αν
Άρα αν  με
με  Εύκολα βλέπουμε ότι από τη συνέχεια της
Εύκολα βλέπουμε ότι από τη συνέχεια της  για κάθε
για κάθε  και
και  για κάθε
για κάθε  Επομένως το
Επομένως το 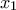 είναι θέση τοπικού
είναι θέση τοπικού  είναι θέση τοπικού ελαχίστου.
είναι θέση τοπικού ελαχίστου. Επομένως,
Επομένως,  δηλαδή
δηλαδή  και
και Είναι φανερό τώρα ότι η
Είναι φανερό τώρα ότι η  έχει εξίσωση
έχει εξίσωση  .
.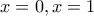 ενώ το
ενώ το 
 για την οποία ισχύει
για την οποία ισχύει 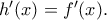
 έχουμε δείξει στο 2 ότι
έχουμε δείξει στο 2 ότι  οπότε η
οπότε η  είναι
είναι 

 (από
(από  αφού τότε
αφού τότε  με ισότητα μόνο για
με ισότητα μόνο για  η
η  (έχουν ίδια παράγωγο άρα οι εξισώσεις
(έχουν ίδια παράγωγο άρα οι εξισώσεις 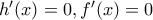
 είναι
είναι  και
και 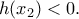 Από
Από  και ο γεγονός ότι η
και ο γεγονός ότι η  παίρνουμε
παίρνουμε 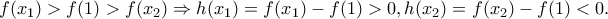 Το τελευταίο αποτέλεσμα σε
Το τελευταίο αποτέλεσμα σε 