Να βρεθεί το
 .
.Ευχαριστώ.
Συντονιστής: KAKABASBASILEIOS
Για
 θεωρούμε τη συνάρτηση
θεωρούμε τη συνάρτηση  . H
. H  είναι συνεχής και παραγωγίσιμη στο
είναι συνεχής και παραγωγίσιμη στο  και ικανοποιεί τις προϋποθέσεις του Θεωρήματος Μέσης Τιμής στο διάστημα
και ικανοποιεί τις προϋποθέσεις του Θεωρήματος Μέσης Τιμής στο διάστημα ![[x^2, x^2+1] [x^2, x^2+1]](/forum/ext/geomar/texintegr/latexrender/pictures/20b186ba7ca15d0e1db024828684112b.png) . Συνεπώς υπάρχει
. Συνεπώς υπάρχει  τέτοιο ώστε
τέτοιο ώστε
 . Συνεπώς ,
. Συνεπώς , 
 Γιατί;
Γιατί;
Καλησπέρα σε όλους.Tolaso J Kos έγραψε: ↑Τετ Οκτ 17, 2018 12:11 pmΓιαθεωρούμε τη συνάρτηση
. H
είναι συνεχής και παραγωγίσιμη στο
και ικανοποιεί τις προϋποθέσεις του Θεωρήματος Μέσης Τιμής στο διάστημα
. Συνεπώς υπάρχει
τέτοιο ώστε

Όμως,. Συνεπώς ,

Γιατί;
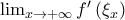 .
.  . Π.χ. είναι συνεχής συνάρτηση του
. Π.χ. είναι συνεχής συνάρτηση του  ή η συμπεριφορά της στο άπειρο ακολουθεί τους κανόνες των ακολουθιών, των οποίων το Π.Ο. είναι σύνολο διακριτών τιμών;
ή η συμπεριφορά της στο άπειρο ακολουθεί τους κανόνες των ακολουθιών, των οποίων το Π.Ο. είναι σύνολο διακριτών τιμών; Καλό βράδυ.Γιώργος Ρίζος έγραψε: ↑Παρ Οκτ 19, 2018 8:41 pm
Καλησπέρα σε όλους.
Αν είναι εύκολο, ας δώσει κάποιος μερικές πληροφορίες (και βιβλιογραφία) σχετικές με την τεχνική του Αποστόλη στο σημείο όπου υπολογίζεται το όριο του.
Ο προβληματισμός μου έχει να κάνει με τις ιδιότητες του. Π.χ. είναι συνεχής συνάρτηση του
ή η συμπεριφορά της στο άπειρο ακολουθεί τους κανόνες των ακολουθιών, των οποίων το Π.Ο. είναι σύνολο διακριτών τιμών;
Τεκμηριώνεται αυτό με την ύλη των "σχολικών μαθηματικών";
Ομολογώ ότι δεν θυμάμαι να έχω ξανασυναντήσει αυτήν την τεχνική, γι' αυτό αναζητώ πληροφορίες.
Ευχαριστώ προκαταβολικά.
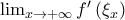 υπάρχει γιατί υπάρχει το όριο της παραγώγου. Εν γένει όταν εφαρμόζουμε ΘΜΤ σε
υπάρχει γιατί υπάρχει το όριο της παραγώγου. Εν γένει όταν εφαρμόζουμε ΘΜΤ σε ![[f(x),g(x)] [f(x),g(x)]](/forum/ext/geomar/texintegr/latexrender/pictures/64b4e28e8cd09349ea4a64d77a3b6b56.png) για κάθε
για κάθε  μπορεί να περιέχονται στο διάστημα παραπάνω από ένα
μπορεί να περιέχονται στο διάστημα παραπάνω από ένα  . Επιλέγοντας ένα
. Επιλέγοντας ένα  Στο συγκεκριμένο παράδειγμα η
Στο συγκεκριμένο παράδειγμα η  , στο διάστημα
, στο διάστημα  το
το  είναι μοναδικό (και συνεχής συνάρτηση). Σχολική δεν την θεωρώ τη
είναι μοναδικό (και συνεχής συνάρτηση). Σχολική δεν την θεωρώ τη  και πέρα είναι γνησίως αύξουσα οπότε
και πέρα είναι γνησίως αύξουσα οπότε 
Ευχαριστώ τον Λάμπρο για την κατατοπιστική επεξήγηση και τον Αποστόλη για το προσωπικό μήνυμα που μού έστειλε.Λάμπρος Κατσάπας έγραψε: ↑Παρ Οκτ 19, 2018 10:50 pm
Σχολική δεν την θεωρώ τη λύση μιας και το σημείο αυτό είναι αρκετά λεπτό.
Καλημέρα Γιώργο.Γιώργος Ρίζος έγραψε: ↑Κυρ Οκτ 21, 2018 10:04 am
Η παρέμβασή μου έχει να κάνει με τη συμβατότητα της λύσης με το περιεχόμενο της "σχολικής" ύλης και των εργαλείων που νομιμοποιούνται να χρησιμοποιήσουν οι μαθητές, εφόσον η συζήτηση γίνεται σε "μαθητικό φάκελο".
Καλημέρα σε όλους.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Κυρ Οκτ 21, 2018 11:08 am
Δεν καταλαβαίνω γιατί οι μαθητές δεν νομιμοποιούνται να χρησιμοποιήσουν εργαλεία που δεν είναι
στην σχολική ύλη.
Στις οδηγίες στο τέλος γράφει
''Κάθε απάντηση επιστημονικά τεκμηριωμένη είναι αποδεκτή''
Αν ήταν έτσι όπως το γράφεις νομίζω ότι θα έπρεπε να γράφει
Κάθε απάντηση επιστημονικά τεκμηριωμένη στα πλαίσια της σχολικής ύλης είναι αποδεκτή
Λάμπρος Κατσάπας έγραψε: ↑Παρ Οκτ 19, 2018 10:50 pm
(...) Επιλέγοντας ένα από αυτά (μπορούμε να το κάνουμε με βάση γνωστό αξίωμα) μπορούμε να ορίσουμε συνάρτησηΣτο συγκεκριμένο παράδειγμα η συνάρτηση από μια πρόχειρη γραφική παράσταση που έκανα είναι κυρτή και για προφανείς λόγους (μπορεί να το καταλάβει κάποιος γεωμετρικά αλλά αποδεικνύεται κιόλας), για κάθε
, στο διάστημα
το
είναι μοναδικό (και συνεχής συνάρτηση). Σχολική δεν την θεωρώ τη λύση μιας και το σημείο αυτό είναι αρκετά λεπτό.
Το μόνο που χρειάζεται για να τεκμηριωθεί επιστημονικά αυτή η λύση είναι ο ορισμός του ορίου στοΓιώργος Ρίζος έγραψε: ↑Παρ Οκτ 19, 2018 8:41 pmΚαλησπέρα σε όλους.Tolaso J Kos έγραψε: ↑Τετ Οκτ 17, 2018 12:11 pmΓιαθεωρούμε τη συνάρτηση
. H
είναι συνεχής και παραγωγίσιμη στο
και ικανοποιεί τις προϋποθέσεις του Θεωρήματος Μέσης Τιμής στο διάστημα
. Συνεπώς υπάρχει
τέτοιο ώστε

Όμως,. Συνεπώς ,

Γιατί;
Αν είναι εύκολο, ας δώσει κάποιος μερικές πληροφορίες (και βιβλιογραφία) σχετικές με την τεχνική του Αποστόλη στο σημείο όπου υπολογίζεται το όριο του.
Ο προβληματισμός μου έχει να κάνει με τις ιδιότητες του. Π.χ. είναι συνεχής συνάρτηση του
ή η συμπεριφορά της στο άπειρο ακολουθεί τους κανόνες των ακολουθιών, των οποίων το Π.Ο. είναι σύνολο διακριτών τιμών;
Τεκμηριώνεται αυτό με την ύλη των "σχολικών μαθηματικών";
Ομολογώ ότι δεν θυμάμαι να έχω ξανασυναντήσει αυτήν την τεχνική, γι' αυτό αναζητώ πληροφορίες.
Ευχαριστώ προκαταβολικά.
 μιας συνάρτησης.Δεν έχει σημασία αν η συνάρτηση
μιας συνάρτησης.Δεν έχει σημασία αν η συνάρτηση  είναι συνεχής η όχι.Αρκεί να ισχύει
είναι συνεχής η όχι.Αρκεί να ισχύει  και τότε εφαρμόζεις τον ορισμό του ορίου στο
και τότε εφαρμόζεις τον ορισμό του ορίου στο  και έχεις
και έχεις 
 .
. και το
και το  είναι σημείο συσσώρευσης του
είναι σημείο συσσώρευσης του  τότε έχουμε
τότε έχουμε  καθώς
καθώς  αν και μόνο αν για κάθε
αν και μόνο αν για κάθε  υπάρχει
υπάρχει  ώστε για κάθε
ώστε για κάθε  με
με 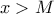 έχουμε
έχουμε  .
. αλλά δεν νομίζω να του έκοβε καμία μονάδα ο διορθωτής αν δεν το έγραφε αυτό ο μαθητής.Το αξίωμα της επιλογής χρησιμοποιείται σιωπηρά στα σύγχρονα μαθηματικά πολλές φορές και δεν χρειάζεται να το αναφέρεις κάθε φορά που το χρησιμοποιείς.
αλλά δεν νομίζω να του έκοβε καμία μονάδα ο διορθωτής αν δεν το έγραφε αυτό ο μαθητής.Το αξίωμα της επιλογής χρησιμοποιείται σιωπηρά στα σύγχρονα μαθηματικά πολλές φορές και δεν χρειάζεται να το αναφέρεις κάθε φορά που το χρησιμοποιείς.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες