 παραγωγίσημη
παραγωγίσημηΑν η εφαπτομένη σε κάθε σημείο της

διέρχεται από σταθερό σημείο να δειχθεί ότι η
 είναι μέρος ευθείας
είναι μέρος ευθείαςΣυντονιστής: KAKABASBASILEIOS
 παραγωγίσημη
παραγωγίσημη
 είναι μέρος ευθείας
είναι μέρος ευθείαςΑνΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Τετ Οκτ 31, 2018 8:57 amΕστωπαραγωγίσημη
Αν η εφαπτομένη σε κάθε σημείο της
διέρχεται από σταθερό σημείο να δειχθεί ότι ηείναι μέρος ευθείας
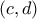 το σταθερό σημείο και
το σταθερό σημείο και 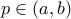 τυχαίο, η υπόθεση είναι ότι η
τυχαίο, η υπόθεση είναι ότι η  διέρχεται
διέρχεται 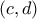 . 'Αρα
. 'Αρα  .
. . Οι άλλες περιπτώσεις είναι όμοιες και ευκολότερες (βλέπε παρακάτω).
. Οι άλλες περιπτώσεις είναι όμοιες και ευκολότερες (βλέπε παρακάτω).  ) και γράφουμε
) και γράφουμε  . Για
. Για  είναι
είναι  ή αλλιώς
ή αλλιώς 
 με
με  για
για  και
και  για
για 
 για
για  και
και 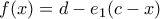 για
για  . Από παραγωγισιμότητα,
. Από παραγωγισιμότητα,  , και λοιπά.
, και λοιπά. δεν ήταν στο διάστημα
δεν ήταν στο διάστημα  θα γλιτώναμε αυτό το βήμα καθώς περιττεύουν οι συνθήκες
θα γλιτώναμε αυτό το βήμα καθώς περιττεύουν οι συνθήκες  για
για  στο
στο  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 12 επισκέπτες