exdx έγραψε: ↑Τετ Νοέμ 14, 2018 12:29 pm
Δίνεται η συνάρτηση

και το τυχαίο σημείο

της

.
Έστω

η εφαπτόμενη ευθεία της

στο

η οποία τέμνει τον άξονα
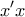
στο σημείο

.
α) Nα αποδείξετε ότι υπάρχει μοναδική θέση του

ώστε η απόσταση
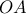
να γίνεται ελάχιστη .
β) Να βρείτε τις τιμές του

για τις οποίες το
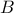
έχει αρνητική τετμημένη .
γ) Αν το
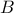
έχει αρνητική τετμημένη , να βρείτε το

ώστε το εμβαδόν του τριγώνου

να είναι το μέγιστο δυνατό .
δ) Αν το

έχει αρνητική τετμημένη και απομακρύνεται από τον

με ταχύτητα

να βρείτε το ρυθμό μεταβολής
του εμβαδού του τριγώνου

τη στιγμή που αυτό είναι ισοσκελές .
...επειδή παρουσιάζει εξεταστικό ενδιαφέρον, δίνω μιά αντιμετώπιση....
ΛΥΣΗ
α) Είναι η απόσταση

που είναι συνάρτηση παραγωγίσιμη με

και για την συνάρτηση του αριθμητή

που είναι συνεχής με

σύμφωνα με το θεώρημα του Bolzano υπάρχει

με

που είναι και μοναδική αφού

άρα η

γνήσια αύξουσα και

έτσι για την

είναι για

δηλαδή η

είναι γνήσια φθίνουσα στο
![(-\infty ,\,\,{{x}_{0}}] (-\infty ,\,\,{{x}_{0}}]](/forum/ext/geomar/texintegr/latexrender/pictures/b179798d8e8da6c1d08acd8a95202f79.png)
και για

δηλαδή
η

είναι γνήσια αύξουσα στο

έτσι στο

είναι η μοναδική θέση του

ώστε η απόσταση
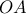
να γίνεται ελάχιστη .
β) Η εφαπτομένη στο

είναι

και αν το

είναι το σημείο τομής με τον άξονα
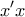
ισχύει ότι

και είναι
 γ)
γ) Το εμβαδό του τριγώνου

και θεωρώντας την συνάρτηση

έχουμε ότι
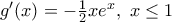
που είναι

άρα

γνήσια φθίνουσα στο
![[0,\,\,1] [0,\,\,1]](/forum/ext/geomar/texintegr/latexrender/pictures/64486b1bb1fcabef4d7394f4c4b2a10d.png)
και

άρα

γνήσια αύξουσα στο
![(-\infty ,\,0] (-\infty ,\,0]](/forum/ext/geomar/texintegr/latexrender/pictures/6bfc829fcc1383870609719428b1135d.png)
επομένως στη θέση

έχουμε το εμβαδόν του τριγώνου

να είναι το μέγιστο δυνατό.
δ) ...ισοσκελές σε ποιες πλευρές;;;;;....
Φιλικά και Μαθηματικά
Βασίλης
 και το τυχαίο σημείο
και το τυχαίο σημείο  της
της  .
. η εφαπτόμενη ευθεία της
η εφαπτόμενη ευθεία της  στο
στο  η οποία τέμνει τον άξονα
η οποία τέμνει τον άξονα  στο σημείο
στο σημείο  .
.  ώστε η απόσταση
ώστε η απόσταση 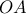 να γίνεται ελάχιστη .
να γίνεται ελάχιστη . για τις οποίες το
για τις οποίες το 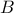 έχει αρνητική τετμημένη .
έχει αρνητική τετμημένη .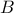 έχει αρνητική τετμημένη , να βρείτε το
έχει αρνητική τετμημένη , να βρείτε το  ώστε το εμβαδόν του τριγώνου
ώστε το εμβαδόν του τριγώνου  να είναι το μέγιστο δυνατό .
να είναι το μέγιστο δυνατό . έχει αρνητική τετμημένη και απομακρύνεται από τον
έχει αρνητική τετμημένη και απομακρύνεται από τον  με ταχύτητα
με ταχύτητα  να βρείτε το ρυθμό μεταβολής
να βρείτε το ρυθμό μεταβολής  τη στιγμή που αυτό είναι ισοσκελές .
τη στιγμή που αυτό είναι ισοσκελές .
 που είναι συνάρτηση παραγωγίσιμη με
που είναι συνάρτηση παραγωγίσιμη με  και για την συνάρτηση του αριθμητή
και για την συνάρτηση του αριθμητή 
 σύμφωνα με το θεώρημα του Bolzano υπάρχει
σύμφωνα με το θεώρημα του Bolzano υπάρχει  με
με  που είναι και μοναδική αφού
που είναι και μοναδική αφού  άρα η
άρα η  γνήσια αύξουσα και
γνήσια αύξουσα και  έτσι για την
έτσι για την  είναι για
είναι για  δηλαδή η
δηλαδή η 
![(-\infty ,\,\,{{x}_{0}}] (-\infty ,\,\,{{x}_{0}}]](/forum/ext/geomar/texintegr/latexrender/pictures/b179798d8e8da6c1d08acd8a95202f79.png) και για
και για  δηλαδή
δηλαδή  έτσι στο
έτσι στο  και αν το
και αν το  είναι το σημείο τομής με τον άξονα
είναι το σημείο τομής με τον άξονα 


 έχουμε ότι
έχουμε ότι 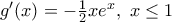
 άρα
άρα ![[0,\,\,1] [0,\,\,1]](/forum/ext/geomar/texintegr/latexrender/pictures/64486b1bb1fcabef4d7394f4c4b2a10d.png) και
και 
![(-\infty ,\,0] (-\infty ,\,0]](/forum/ext/geomar/texintegr/latexrender/pictures/6bfc829fcc1383870609719428b1135d.png) επομένως στη θέση
επομένως στη θέση  έχουμε το εμβαδόν του τριγώνου
έχουμε το εμβαδόν του τριγώνου