 , είναι :
, είναι :  και
και  . Και αναφύεται
. Και αναφύεται το ερώτημα : Το
 είναι πλησιέστερα στο
είναι πλησιέστερα στο  ή στην
ή στην  ; Λοιπόν , για κάθε
; Λοιπόν , για κάθε  ,
,δείξτε ότι ισχύει :

Συντονιστής: KAKABASBASILEIOS
 , είναι :
, είναι :  και
και  . Και αναφύεται
. Και αναφύεται  είναι πλησιέστερα στο
είναι πλησιέστερα στο  ή στην
ή στην  ; Λοιπόν , για κάθε
; Λοιπόν , για κάθε  ,
,
Θεωρώ τη συνάρτηση
 που είναι συνεχής και παραγωγίσιμη στο
που είναι συνεχής και παραγωγίσιμη στο  με
με
 είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο  και
και 

.
 είναι εφαπτόμενη. Παίρνουμε εμβαδά χωρίων. Αρκεί, εν τέλει, το κόκκινο να είναι μικρότερο του μπλε.
είναι εφαπτόμενη. Παίρνουμε εμβαδά χωρίων. Αρκεί, εν τέλει, το κόκκινο να είναι μικρότερο του μπλε. 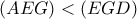

.
 είναι
είναι  (για μεγάλα
(για μεγάλα  στο εν λόγω διάστημα δεν έχει ενδιαφέρον καθώς η εφαπτομένη είναι μεγάλη).
στο εν λόγω διάστημα δεν έχει ενδιαφέρον καθώς η εφαπτομένη είναι μεγάλη).  ήταν γνωστό από τον
ήταν γνωστό από τον  -o αιώνα(!) αλλά δεν μπορώ να θυμηθώ ποιος το είχε διατυπώσει.
-o αιώνα(!) αλλά δεν μπορώ να θυμηθώ ποιος το είχε διατυπώσει. 
Mihalis_Lambrou έγραψε: ↑Σάβ Δεκ 08, 2018 2:00 pmΜπορούμε πολύ καλύτερα. Αποδεικνύεται ότι για μικράείναι
 για
για  .
. . Θεωρώ την παραγωγίσιμη
. Θεωρώ την παραγωγίσιμη  :
:  , με
, με  . Στο
. Στο  , είναι :
, είναι : κ.λ.π.
κ.λ.π. , ισχύει :
, ισχύει :  και
και 
.
 για
για  .
. ![\displaystyle 2 \cos {x} +\frac {1}{\cos ^2{x}}-3=2 c +\frac {1}{c^2}-3 = c+ c +\frac {1}{c^2}-3> 3\sqrt [3]{c\cdot c \cdot \frac {1}{c^2}} - 3 = 0 \displaystyle 2 \cos {x} +\frac {1}{\cos ^2{x}}-3=2 c +\frac {1}{c^2}-3 = c+ c +\frac {1}{c^2}-3> 3\sqrt [3]{c\cdot c \cdot \frac {1}{c^2}} - 3 = 0](/forum/ext/geomar/texintegr/latexrender/pictures/c77b33dc7b7a2923059d10f43ba659f5.png) (εδώ
(εδώ  ). Και λοιπά.
). Και λοιπά.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες