 και
και  για κάθε
για κάθε  , τότε
, τότε 
Συντονιστής: KAKABASBASILEIOS
Γιώργη , γνωστή είναι αυτή. Για παράδειγμα ο Μπάρλας την έχει στην ενότητα με το Fermat. Anyway,
 . Τότε είναι
. Τότε είναι  . Επειδή το
. Επειδή το  και η
και η  είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  θα είναι από Fermat
θα είναι από Fermat  . Τότε όμως:
. Τότε όμως:

Γιώργη και


 .
. , παραγωγίσιμη με
, παραγωγίσιμη με  .
.
 ισχύουν οι προϋποθέσεις του Θεωρήματος Fermat.
ισχύουν οι προϋποθέσεις του Θεωρήματος Fermat. .
.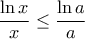
 για κάθε
για κάθε  άρα από Fermat,
άρα από Fermat, 

 και βάλε χρόνια η άσκηση
και βάλε χρόνια η άσκηση  στο CRUX έλεγε:
στο CRUX έλεγε: και ισχύει
και ισχύει 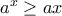 για κάθε
για κάθε  , δείξετε ότι
, δείξετε ότι  .
. ...δύο λύσεις ξεχωριστές από τα συνηθισμένα…Mihalis_Lambrou έγραψε: ↑Σάβ Φεβ 16, 2019 5:39 pmΥπάρχουν και πολλές παραλλαγές της άσκησης. Για παράδειγμα πριν απόκαι βάλε χρόνια η άσκηση
στο CRUX έλεγε:
Ανκαι ισχύει
για κάθε
, δείξετε ότι
.
Ας δούμε λύσεις. Είχα στείλει τότε στο CRUX δύο λύσεις, η μία χωρίς παραγώγους.
 (1)
(1)  και από (1)
και από (1)  και τότε
και τότε  και αν
και αν  είναι
είναι 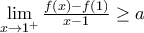 άρα
άρα 
 και από (1)
και από (1)  και τότε
και τότε  και αν
και αν  είναι
είναι  άρα
άρα 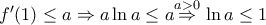 έτσι
έτσι 
 είναι παραγωγίσιμη με
είναι παραγωγίσιμη με  και
και 

 η
η  είναι γνήσια αύξουσα επομένως όταν
είναι γνήσια αύξουσα επομένως όταν  και για
και για  επομένως στο
επομένως στο  η συνάρτηση παρουσιάζει ελάχιστο το
η συνάρτηση παρουσιάζει ελάχιστο το 
 από τα δεδομένα είναι και
από τα δεδομένα είναι και  και με
και με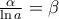 έχουμε ότι είναι
έχουμε ότι είναι  απ όπου
απ όπου  (γιατί από αρχική ανισότητα
(γιατί από αρχική ανισότητα 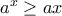 είναι
είναι  ) και επειδή από
) και επειδή από 
 με όπου
με όπου  το
το 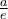 ισχύει
ισχύει 
 που ισχύει μόνο όταν
που ισχύει μόνο όταν 
Αλλιώς: ΓράφονταςMihalis_Lambrou έγραψε: ↑Σάβ Φεβ 16, 2019 5:39 pmΥπάρχουν και πολλές παραλλαγές της άσκησης. Για παράδειγμα πριν απόκαι βάλε χρόνια η άσκηση
στο CRUX έλεγε:
Ανκαι ισχύει
για κάθε
, δείξετε ότι
.
Ας δούμε λύσεις. Είχα στείλει τότε στο CRUX δύο λύσεις, η μία χωρίς παραγώγους.
 η δοθείσα γίνεται
η δοθείσα γίνεται  .
. γίνεται
γίνεται 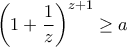 .
. .
. 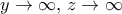 έπεται
έπεται 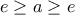 , από όπου το ζητούμενο.
, από όπου το ζητούμενο.ΗMihalis_Lambrou έγραψε: ↑Σάβ Φεβ 16, 2019 5:39 pmΥπάρχουν και πολλές παραλλαγές της άσκησης. Για παράδειγμα πριν απόκαι βάλε χρόνια η άσκηση
στο CRUX έλεγε:
Ανκαι ισχύει
για κάθε
, δείξετε ότι
.
Ας δούμε λύσεις. Είχα στείλει τότε στο CRUX δύο λύσεις, η μία χωρίς παραγώγους.
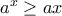 για κάθε
για κάθε  ισοδυναμεί με την
ισοδυναμεί με την 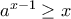 για κάθε
για κάθε  που ισοδυναμεί με την
που ισοδυναμεί με την  για κάθε
για κάθε  . Η τελευταία συνεπάγεται την
. Η τελευταία συνεπάγεται την 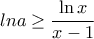 για κάθε
για κάθε 
 για κάθε
για κάθε  .
.  και
και 
 και
και  δηλαδή
δηλαδή 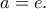
 , για κάθε
, για κάθε  . Από Fermat , υπάρχει
. Από Fermat , υπάρχει  ώστε
ώστε

 ισχύει
ισχύει  και
και . Άρα έχει μοναδική λύση την
. Άρα έχει μοναδική λύση την  οπότε
οπότε 
 δίδεται
δίδεται  , ισοδύναμα
, ισοδύναμα  . Δηλαδή
. Δηλαδή  ολικό ελάχιστο και άρα
ολικό ελάχιστο και άρα  . Το τελευταίο γράφεται
. Το τελευταίο γράφεται  . Απλοποιώντας το
. Απλοποιώντας το  , έχουμε
, έχουμε  , οπότε
, οπότε  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες