
παραγωγίσιμη , γνησίως αύξουσα και κυρτή. Να βρεθεί το :

Συντονιστής: KAKABASBASILEIOS
Καλησπέρα :
 η παράγωγος είναι θετική.Παίρνουμε την εφαπτομένη σε αυτό το σημείο που είναι της μορφής
η παράγωγος είναι θετική.Παίρνουμε την εφαπτομένη σε αυτό το σημείο που είναι της μορφής  .Λόγω της κυρτότητας είναι
.Λόγω της κυρτότητας είναι  για κάθε
για κάθε  .Αυτή η σχέση δίνει ότι το όριο είναι
.Αυτή η σχέση δίνει ότι το όριο είναι  ,αφού η ''μικρή'' συνάρτηση απειρίζεται καθώς το
,αφού η ''μικρή'' συνάρτηση απειρίζεται καθώς το  απειρίζεται θετικά..
απειρίζεται θετικά..Επειδή μάλλον είναι άσκηση στο σπίτι από μαθήματα που παρακολουθείς, ας αρκεστούμε για την ώρα σε
 . β) Από κυρτότητα είναι
. β) Από κυρτότητα είναι 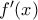 γνήσια αύξουσα.
γνήσια αύξουσα. ![\left [ 0 ,\right x] \left [ 0 ,\right x]](/forum/ext/geomar/texintegr/latexrender/pictures/8f0223ceabdac4d95758ad4bb288a81f.png) και χρησιμοποιώντας την μονοτονία της παραγώγου στην ανίσωση
και χρησιμοποιώντας την μονοτονία της παραγώγου στην ανίσωση  κατέληξα στο εξής :
κατέληξα στο εξής :  (1) Έδωσα την εξής αιτιολόγηση : Αφού η παράγωγος γνησίως αύξουσα , τότε είναι 1-1 . Άρα η εξίσωση
(1) Έδωσα την εξής αιτιολόγηση : Αφού η παράγωγος γνησίως αύξουσα , τότε είναι 1-1 . Άρα η εξίσωση 
 γνησίως αύξουσα και συνεχής , άρα
γνησίως αύξουσα και συνεχής , άρα 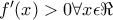 εκτός ίσως από ένα
εκτός ίσως από ένα  ,ρίζα της παραγώγου. Αν
,ρίζα της παραγώγου. Αν  τότε , θέτωντας στην σχέση (1) όπου x το 0 καταλήγουμε σε άτοπο .
τότε , θέτωντας στην σχέση (1) όπου x το 0 καταλήγουμε σε άτοπο .  , το οποίο είναι άτοπο. Άρα η παράγωγος δεν έχει ρίζες στο
, το οποίο είναι άτοπο. Άρα η παράγωγος δεν έχει ρίζες στο ![\left [ 0, \right +\infty ] \left [ 0, \right +\infty ]](/forum/ext/geomar/texintegr/latexrender/pictures/0d2f31d4bd9f6e86246f43b637f15624.png)
Μέσες άκρες σωστά, αλλά υπάρχουν πολλά περιττά. Πιο λιτά:Agnwsth έγραψε: ↑Σάβ Φεβ 16, 2019 10:12 pmΚαλησπέρα. Ευχαριστώ για τις υποδείξεις σας. όταν έλυσα την άσκηση δεν σκέφτηκα καθόλου την εφαπτομένη, και έτσι η λύση βγήκε πολύ σύνθετη. Αυτός ήταν και ο λόγος που απευθύνθηκα εδώ, γιατί σκέφτηκα ότι θα υπάρχει και πιο απλός τρόπος.
Χρησιμοποίησα το Θ.Μ.Τ. στοκαι χρησιμοποιώντας την μονοτονία της παραγώγου στην ανίσωση
κατέληξα στο εξής :
(1) Έδωσα την εξής αιτιολόγηση : Αφού η παράγωγος γνησίως αύξουσα , τότε είναι 1-1 . Άρα η εξίσωση
έχει το πολύ μια ρίζα. Δηλαδή, δεν συγκροτείται διάστημα από το πλήθος των ριζών της παραγώγου, και ηγνησίως αύξουσα και συνεχής , άρα
εκτός ίσως από ένα
,ρίζα της παραγώγου. Αν
τότε , θέτωντας στην σχέση (1) όπου x το 0 καταλήγουμε σε άτοπο .
Αν, το οποίο είναι άτοπο. Άρα η παράγωγος δεν έχει ρίζες στο
Ύστερα χρησιμοποιώ το κριτήριο παρεμβολής..
 τέτοιο ώστε
τέτοιο ώστε  . Τώρα, και πάλι εύκολα, για
. Τώρα, και πάλι εύκολα, για  έχουμε
έχουμε  . Τέλος, παίρνουμε όριο
. Τέλος, παίρνουμε όριο  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Google [Bot] και 4 επισκέπτες