KARKAR έγραψε: ↑Δευ Δεκ 14, 2020 2:22 pm
Η παρέμβαση του Μιχάλη , χρησιμότατη .
Όμως , κατέταξε το θέμα στα "απαντημένα" , με αποτέλεσμα να μείνει αναπάντητο .
Το επαναφέρω λοιπόν , κυρίως για το δεύτερο ερώτημα ...
Αναπάντητο, ε; Σαν
το δικό μου δηλαδή

Λοιπόν για το πρώτο ερώτημα ... Κάνω ότι δεν ξέρω πως πρόκειται για την

... και απλά αναζητώ

με την ζητούμενη ιδιότητα, να ισούται δηλαδή η τετμημένη

του σημείου τομής της εφαπτομένης της

στο

,

, με τον άξονα των

προς

: αναζητούμε δηλαδή

τέτοια ώστε να ισχύει, για κάθε

, η (διαφορική) εξίσωση

.
Προφανώς η

ικανοποιεί την παραπάνω (διαφορική) εξίσωση, που εύκολα βέβαια επιλύεται -- λυκειακά νομίζω -- μέσω της

.
Για το δεύτερο ερώτημα τώρα ... θέλουμε, σύμφωνα και με τα παραπάνω, να έχει μοναδική λύση για

η εξίσωση

. Θεωρώντας την

παρατηρούμε ότι η

ισούται προς

στο

και τείνει στο

όταν το

τείνει στο

, αρκεί επομένως να δείξουμε ότι η

έχει μοναδικό σημείο τοπικού ελαχίστου στο οποίο λαμβάνει αρνητική τιμή. Αρκεί δηλαδή να δείξουμε ότι υπάρχει μοναδικό

τέτοιο ώστε

&

και

, δηλαδή

&

και

: προφανώς

είναι μοναδική λύση για τις

&

, ενώ ικανοποιεί και την

λόγω της
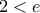
.
Κάπου λοιπόν ανάμεσα στο

και στο

υπάρχει ένα και μοναδικό

τέτοιο ώστε

. Επειδή η

είναι γνησίως αύξουσα για

λόγω της

, αρκεί για το ζητούμενο

να δείξουμε ότι ισχύει η

, δηλαδή η

, ισοδύναμη προς την

, που ισχύει λόγω της δοθείσης

και της

.
 Σε τυχόν σημείο
Σε τυχόν σημείο  της γραφικής παράστασης της
της γραφικής παράστασης της  , με θετική τετμημένη , φέρω εφαπτομένη
, με θετική τετμημένη , φέρω εφαπτομένη  και
και  . Είναι σχεδόν γνωστό
. Είναι σχεδόν γνωστό είναι συμμετρικά ως προς
είναι συμμετρικά ως προς  . Αφού δεν το θυμάστε , δείξτε το !
. Αφού δεν το θυμάστε , δείξτε το ! . Όμως και γι' αυτή , υπάρχει σημείο
. Όμως και γι' αυτή , υπάρχει σημείο  με αυτήν την ιδιότητα .
με αυτήν την ιδιότητα . . Δίνεται ότι :
. Δίνεται ότι : 


 ... και απλά αναζητώ
... και απλά αναζητώ  με την ζητούμενη ιδιότητα, να ισούται δηλαδή η τετμημένη
με την ζητούμενη ιδιότητα, να ισούται δηλαδή η τετμημένη  του σημείου τομής της εφαπτομένης της
του σημείου τομής της εφαπτομένης της  ,
,  , με τον άξονα των
, με τον άξονα των  προς
προς  : αναζητούμε δηλαδή
: αναζητούμε δηλαδή  , η (διαφορική) εξίσωση
, η (διαφορική) εξίσωση .
. .
. . Θεωρώντας την
. Θεωρώντας την  παρατηρούμε ότι η
παρατηρούμε ότι η  ισούται προς
ισούται προς  στο
στο  όταν το
όταν το  τείνει στο
τείνει στο  &
&  και
και  , δηλαδή
, δηλαδή  &
&  και
και  : προφανώς
: προφανώς  είναι μοναδική λύση για τις
είναι μοναδική λύση για τις 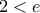 .
. και στο
και στο  τέτοιο ώστε
τέτοιο ώστε  . Επειδή η
. Επειδή η  λόγω της
λόγω της  , αρκεί για το ζητούμενο
, αρκεί για το ζητούμενο  να δείξουμε ότι ισχύει η
να δείξουμε ότι ισχύει η  , δηλαδή η
, δηλαδή η  , ισοδύναμη προς την
, ισοδύναμη προς την  , που ισχύει λόγω της δοθείσης
, που ισχύει λόγω της δοθείσης  και της
και της  .
.


 βρίσκεται κοντά στο
βρίσκεται κοντά στο