 δύο φορές παραγωγίσιμη στο
δύο φορές παραγωγίσιμη στο  με
με 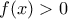 για κάθε
για κάθε  . Αν για κάθε
. Αν για κάθε  ισχύουν
ισχύουν
τότε:
(α) να δειχθεί ότι η
 είναι κυρτή στο
είναι κυρτή στο  .
.(β)
 για κάθε
για κάθε 
(γ) να υπολογιστεί το όριο
 .
.Συντονιστής: KAKABASBASILEIOS
 δύο φορές παραγωγίσιμη στο
δύο φορές παραγωγίσιμη στο  με
με 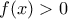 για κάθε
για κάθε  . Αν για κάθε
. Αν για κάθε  ισχύουν
ισχύουν
 είναι κυρτή στο
είναι κυρτή στο  .
. για κάθε
για κάθε 
 .
.
 λογω της δεδομένης ανίσωσης και
λογω της δεδομένης ανίσωσης και 
 κυρτή
κυρτή η
η  η
η  η απο ΘΜΤ
η απο ΘΜΤ  που ισχυει αφου
που ισχυει αφου  κυρτή
κυρτή οταν
οταν 

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 4 επισκέπτες