 είναι ισοσκελές με ύψος
είναι ισοσκελές με ύψος  και
και 
Ποια θέση του
 ελαχιστοποιεί το γαλάζιο εμβαδόν ;
ελαχιστοποιεί το γαλάζιο εμβαδόν ;Συντονιστής: KAKABASBASILEIOS
 είναι ισοσκελές με ύψος
είναι ισοσκελές με ύψος  και
και 
 ελαχιστοποιεί το γαλάζιο εμβαδόν ;
ελαχιστοποιεί το γαλάζιο εμβαδόν ; .
.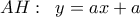 και
και  , οπότε το
, οπότε το  έχει τετμημένη
έχει τετμημένη  , όσο και η απόστασή του από τη
, όσο και η απόστασή του από τη  .
. , που γράφεται
, που γράφεται  .
. 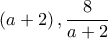 είναι σταθερό, το άθροισμά τους γίνεται ελάχιστο, όταν είναι ίσοι, αν μπορεί να γίνουν ίσοι.
είναι σταθερό, το άθροισμά τους γίνεται ελάχιστο, όταν είναι ίσοι, αν μπορεί να γίνουν ίσοι.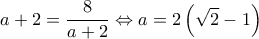 .
. φέρνουμε την παράλληλο προς την
φέρνουμε την παράλληλο προς την  η οποία τέμνει την
η οποία τέμνει την  στο
στο  και την
και την  στο
στο  .
.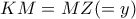 και από τις αναλογίες
και από τις αναλογίες  ,
,  βρίσκουμε ότι:
βρίσκουμε ότι:
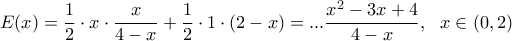
 προκύπτει όταν
προκύπτει όταν  ,
,  απέχει από το
απέχει από το  απόσταση ίση με
απόσταση ίση με 


Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες