
Τότε :

Συντονιστής: KAKABASBASILEIOS
Όμορφη! Σωστή επιλογή είναι η C, δηλαδή είναι
 . Έστω
. Έστω  .
. . Θέλουμε να αποδείξουμε ότι
. Θέλουμε να αποδείξουμε ότι  , ισοδύναμα ότι
, ισοδύναμα ότι  . Έστω η συνάρτηση
. Έστω η συνάρτηση  με
με  . Θέλουμε να αποδείξουμε ότι
. Θέλουμε να αποδείξουμε ότι  .
.  . Έστω
. Έστω  . Τότε, είναι
. Τότε, είναι  .
.![x \in [0,\sqrt{2}-1] x \in [0,\sqrt{2}-1]](/forum/ext/geomar/texintegr/latexrender/pictures/4f78f5b9118e30377facd1c8a0b03d8b.png) είναι
είναι  , άρα η
, άρα η  είναι γνησίως αύξουσα, ενώ για
είναι γνησίως αύξουσα, ενώ για  είναι
είναι  , άρα η
, άρα η  είναι γνησίως φθίνουσα.
είναι γνησίως φθίνουσα.
 ,
,
 και
και
 . Άρα υπάρχει
. Άρα υπάρχει  όσο κοντά στο
όσο κοντά στο  θέλουμε με
θέλουμε με  .
. , από το Θεώρημα Bolzano συμπεραίνουμε ότι υπάρχει
, από το Θεώρημα Bolzano συμπεραίνουμε ότι υπάρχει  τέτοιο, ώστε
τέτοιο, ώστε  , και λόγω της μονοτονίας της
, και λόγω της μονοτονίας της  στο διάστημα αυτό είναι μοναδικό.
στο διάστημα αυτό είναι μοναδικό. έχουμε ότι:
έχουμε ότι:
 για κάθε
για κάθε ![x \in [0,\xi] x \in [0,\xi]](/forum/ext/geomar/texintegr/latexrender/pictures/6ae40eb6bab859c226f70aae0ddfea25.png) και
και
 για κάθε
για κάθε  .
. και
και  , η συνάρτηση
, η συνάρτηση  είναι γνησίως αύξουσα για
είναι γνησίως αύξουσα για ![x \in [0,\xi] x \in [0,\xi]](/forum/ext/geomar/texintegr/latexrender/pictures/6ae40eb6bab859c226f70aae0ddfea25.png) και γνησίως φθίνουσα για
και γνησίως φθίνουσα για  , όπου το
, όπου το  είναι τέτοιο, ώστε
είναι τέτοιο, ώστε  .
.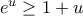 , προκύπτει λοιπόν ότι:
, προκύπτει λοιπόν ότι:
 , δηλαδή
, δηλαδή  .
. , λόγω της μονοτονίας της
, λόγω της μονοτονίας της  προκύπτει ότι
προκύπτει ότι  που δίνει το ζητούμενο.
που δίνει το ζητούμενο. . Θέλουμε να αποδείξουμε ότι
. Θέλουμε να αποδείξουμε ότι 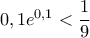 , ισοδύναμα ότι
, ισοδύναμα ότι  , δηλαδή ότι
, δηλαδή ότι  . Θεωρούμε την συνάρτηση
. Θεωρούμε την συνάρτηση 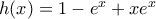 με
με  . Είναι,
. Είναι,
 είναι γνησίως αύξουσα στο πεδίο ορισμού της, οπότε αφού
είναι γνησίως αύξουσα στο πεδίο ορισμού της, οπότε αφού  , είναι
, είναι
 , όπως θέλαμε.
, όπως θέλαμε.Είναι



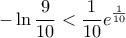





 θα είναι
θα είναι 
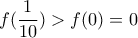













Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες