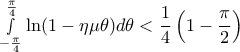
2004 Hirosaki University
Συντονιστής: R BORIS
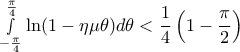
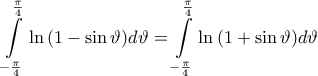 .
.![\displaystyle{\displaystyle
\cos ^2 \vartheta = \left( {1 - \sin \vartheta } \right)\left( {1 + \sin \vartheta } \right) \wedge \cos \vartheta > 0,\forall \vartheta \in \left[ { - \frac{\pi }
{4},\frac{\pi }
{4}} \right]
} \displaystyle{\displaystyle
\cos ^2 \vartheta = \left( {1 - \sin \vartheta } \right)\left( {1 + \sin \vartheta } \right) \wedge \cos \vartheta > 0,\forall \vartheta \in \left[ { - \frac{\pi }
{4},\frac{\pi }
{4}} \right]
}](/forum/ext/geomar/texintegr/latexrender/pictures/bfc16ef445cfb14462cd095ef7d075a1.png) (1).
(1).![\displaystyle{\displaystyle
2\ln \cos \vartheta = \ln \left( {1 - \sin \vartheta } \right) + \ln \left( {1 + \sin \vartheta } \right),\vartheta \in \left[ { - \frac{\pi }
{4},\frac{\pi }
{4}} \right]
} \displaystyle{\displaystyle
2\ln \cos \vartheta = \ln \left( {1 - \sin \vartheta } \right) + \ln \left( {1 + \sin \vartheta } \right),\vartheta \in \left[ { - \frac{\pi }
{4},\frac{\pi }
{4}} \right]
}](/forum/ext/geomar/texintegr/latexrender/pictures/6fd7efcdf8f8e5be2621c4fa4dfac36a.png) . Ολοκληρώνοντας και τα δύο μέλη και μετά απο χρήση του Λήμματος, έχουμε:
. Ολοκληρώνοντας και τα δύο μέλη και μετά απο χρήση του Λήμματος, έχουμε: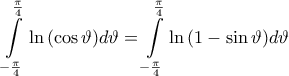 .
.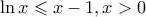 και για x=cosθ>0 έχουμε:
και για x=cosθ>0 έχουμε: 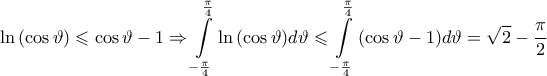 .
.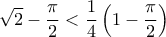 ή καλύτερα:
ή καλύτερα: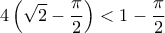 , το οποίο ισχύει... γιατί μετά απο πράξεις καταλήγουμε στη :
, το οποίο ισχύει... γιατί μετά απο πράξεις καταλήγουμε στη : 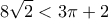 που είναι αληθής (πέρα απο τις αριθμητικές - μπακαλοπράξεις , ψάχνω ακόμα μια πιο αλγεβρική δικαιολογηση)
που είναι αληθής (πέρα απο τις αριθμητικές - μπακαλοπράξεις , ψάχνω ακόμα μια πιο αλγεβρική δικαιολογηση)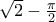
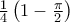 όπου και καλά έκανε για να αποδείξει την σχέση.
όπου και καλά έκανε για να αποδείξει την σχέση.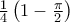 ανακάλυψα ότι προκύπτει από το ολοκλήρωμα
ανακάλυψα ότι προκύπτει από το ολοκλήρωμα 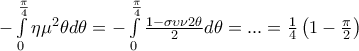
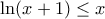 για κάθε x > -1
για κάθε x > -1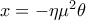 προκύπτει ότι
προκύπτει ότι 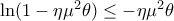
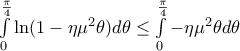
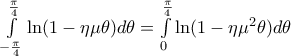 ή
ή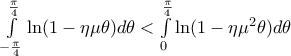
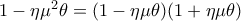
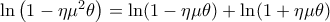
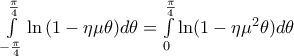
spyrosk έγραψε:
Με το λογισμικό geogebra «φαίνεται» (δεν το έχω αποδείξει) ότι κάνοντας τις γραφικές παραστάσεις των παραπάνω συναρτήσεων προκύπτει ότι
Όπου η απόδειξη του τελειώνει την άσκηση, εδώ λοιπόν χρειάζομαστε την βοήθεια του mathxl ή κάποιου άλλου συναδέλφου.
Άντε νάλθει η Τετάρτη να πιούμε κανένα κρασί γιατί δεν πάει άλλο αυτή η κατάσταση.
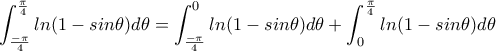
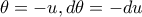 , αλλάζουμε τα άκρα και έχουμε
, αλλάζουμε τα άκρα και έχουμε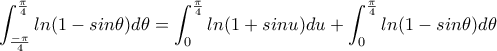
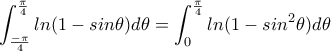
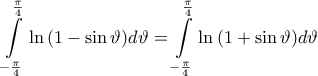 .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες