 . Δείξτε ότι :
. Δείξτε ότι :  .
.Προσπαθήστε να βρείτε και ένα "αξιοπρεπές" άνω φράγμα για το παραπάνω ολοκλήρωμα .
Συντονιστής: R BORIS
 . Δείξτε ότι :
. Δείξτε ότι :  .
.Μήπως δεν βλέπω κάτι; Mε λογισμικό βλέπουμε ότι το ολοκλήρωμα ισούται περίπουKARKAR έγραψε:Δίνεται η συνάρτηση :. Δείξτε ότι :
.
Προσπαθήστε να βρείτε και ένα "αξιοπρεπές" άνω φράγμα για το παραπάνω ολοκλήρωμα .
 που είναι σαφώς μικρότερο από το δοθέν κάτω φράγμα.
που είναι σαφώς μικρότερο από το δοθέν κάτω φράγμα.  που βγαίνει εύκολα από την ιδιότητα
που βγαίνει εύκολα από την ιδιότητα  στο πρώτο τεταρτημόριο.
στο πρώτο τεταρτημόριο. στο πρώτο τεταρτημόριο. Οπότε εύκολα βλέπουμε ότι το ολοκλήρωμα φράσσεται κάτω από το
στο πρώτο τεταρτημόριο. Οπότε εύκολα βλέπουμε ότι το ολοκλήρωμα φράσσεται κάτω από το  .
. και όχι το
και όχι το 



 είναι κοίλη στο
είναι κοίλη στο ![[0,\frac{\pi }{2}] [0,\frac{\pi }{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/274998397c6748353788ed09efdc36d0.png)
 (1)
(1)
 (2)
(2)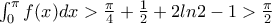
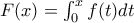
 εχει τοπικά μέγιστα στα
εχει τοπικά μέγιστα στα  και τοπικά ελάχιστα
και τοπικά ελάχιστα  .
.

 είναι στο
είναι στο  και προφανώς
και προφανώς 
![k\left( x \right) = f\left( x \right) - \frac{1}{2}\,/\left[ {0,\,\pi } \right], k\left( x \right) = f\left( x \right) - \frac{1}{2}\,/\left[ {0,\,\pi } \right],](/forum/ext/geomar/texintegr/latexrender/pictures/2c1815537d2ab40539fc9ee1fa690f60.png) είναι γνησίως φθίνουσα , αν αυτό οδηγεί κάπου ...
είναι γνησίως φθίνουσα , αν αυτό οδηγεί κάπου ...![\int_{0}^{\pi} \frac{sinx}{x}dx=\int_{0}^{\pi} \frac{2sin(x/2)cos(x/2)}{x}dx < \int_{0}^{\pi} cos(x/2)dx = [2sin(x/2)]_{0}^{\pi} = 2 \int_{0}^{\pi} \frac{sinx}{x}dx=\int_{0}^{\pi} \frac{2sin(x/2)cos(x/2)}{x}dx < \int_{0}^{\pi} cos(x/2)dx = [2sin(x/2)]_{0}^{\pi} = 2](/forum/ext/geomar/texintegr/latexrender/pictures/19668f421a98fbf7155f210636b96acc.png) .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης