 της γραφικής παράστασης της
της γραφικής παράστασης της 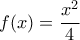 , που βρίσκεται στο πρώτο
, που βρίσκεται στο πρώτοτεταρτημόριο , φέρουμε την κάθετη προς την εφαπτομένη , η οποία ξανατέμνει την

στο σημείο
 . Βρείτε το ελάχιστο εμβαδόν του σχηματιζόμενου γαλάζιου χωρίου .
. Βρείτε το ελάχιστο εμβαδόν του σχηματιζόμενου γαλάζιου χωρίου .Συντονιστής: R BORIS
 της γραφικής παράστασης της
της γραφικής παράστασης της 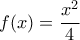 , που βρίσκεται στο πρώτο
, που βρίσκεται στο πρώτο
 . Βρείτε το ελάχιστο εμβαδόν του σχηματιζόμενου γαλάζιου χωρίου .
. Βρείτε το ελάχιστο εμβαδόν του σχηματιζόμενου γαλάζιου χωρίου .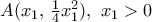 είναι το σημείο της παραβολής,
είναι το σημείο της παραβολής, 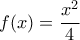 επειδή
επειδή  η εφαπτομένη στο
η εφαπτομένη στο  θα έχει κλίση
θα έχει κλίση  επομένως η κάθετη
επομένως η κάθετη  θα έχει συντελεστή
θα έχει συντελεστή  και εξίσωση
και εξίσωση 
 και της
και της  προκύπτουν από τη λύση του συστήματος
προκύπτουν από τη λύση του συστήματος 

 και
και 
 στον
στον 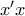 είναι
είναι  και
και 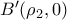 το εμβαδό του χωρίου θα είναι
το εμβαδό του χωρίου θα είναι  να αφαιρέσουμε το εμβαδό του χωρίου που ορίζεται από την παραβολή τον
να αφαιρέσουμε το εμβαδό του χωρίου που ορίζεται από την παραβολή τον 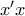
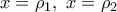 επομένως θα είναι
επομένως θα είναι ![E=\frac{A{A}'+B{B}'}{2}{A}'{B}'-\int\limits_{{{\rho }_{2}}}^{{{\rho }_{1}}}{\frac{1}{4}{{x}^{2}}dx=}\frac{\frac{1}{4}\rho _{1}^{2}+\frac{1}{4}\rho _{2}^{2}}{2}({{\rho }_{1}}-{{\rho }_{2}})-\frac{1}{4}\left[ \frac{{{x}^{3}}}{3} \right]_{{{\rho }_{2}}}^{{{\rho }_{1}}}= E=\frac{A{A}'+B{B}'}{2}{A}'{B}'-\int\limits_{{{\rho }_{2}}}^{{{\rho }_{1}}}{\frac{1}{4}{{x}^{2}}dx=}\frac{\frac{1}{4}\rho _{1}^{2}+\frac{1}{4}\rho _{2}^{2}}{2}({{\rho }_{1}}-{{\rho }_{2}})-\frac{1}{4}\left[ \frac{{{x}^{3}}}{3} \right]_{{{\rho }_{2}}}^{{{\rho }_{1}}}=](/forum/ext/geomar/texintegr/latexrender/pictures/f44bf7f85fcb613f2bef9ccdbd483eda.png)


 και επειδή
και επειδή  τελικά το εμβαδό δίνεται από την συνάρτηση
τελικά το εμβαδό δίνεται από την συνάρτηση  παραγωγίσιμη με
παραγωγίσιμη με 
 στο
στο 
 .
. όπου
όπου 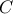 είναι το σημείο τομής των εφαπτομένων στα
είναι το σημείο τομής των εφαπτομένων στα 
 εύκολα
εύκολα και εφάπτεται της
και εφάπτεται της  στο σημείο
στο σημείο 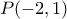 . Το εμβαδόν
. Το εμβαδόν ( βρίσκεται με διάφορους τρόπους ) είναι ίσο με
( βρίσκεται με διάφορους τρόπους ) είναι ίσο με 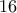 . Αλλά το παραβολικό χωρίο
. Αλλά το παραβολικό χωρίο  του
του  , δηλαδή
, δηλαδή 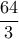 . Βασίλη ευχαριστώ
. Βασίλη ευχαριστώ Υπάρχει σχέση (ευθείας αναλογίας) ανάμεσα στα δύο εμβαδά (τριγώνου και παραβολικού χωρίου); [Οι πράξεις είναι πολλές και διστάζω ... ιδίως αν είναι γνωστό αποτέλεσμα!]
Η λύση απαιτεί πολλές πράξεις . Δίνω μια περίληψη :
 ένα σημείο της παραβολής ,
ένα σημείο της παραβολής , η εφαπτομένη στο
η εφαπτομένη στο 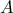 και
και 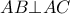

![\displaystyle {{\left[ (AB)(AC) \right]}^{2}}=\left[ {{\left( \frac{2{{x}^{2}}+8}{x} \right)}^{2}}+{{\left( \frac{4{{x}^{2}}+16}{{{x}^{2}}} \right)}^{2}} \right]\left[ {{\left( \frac{{{x}^{2}}+4}{x} \right)}^{2}}+{{\left( \frac{{{x}^{2}}+4}{2} \right)}^{2}} \right] \displaystyle {{\left[ (AB)(AC) \right]}^{2}}=\left[ {{\left( \frac{2{{x}^{2}}+8}{x} \right)}^{2}}+{{\left( \frac{4{{x}^{2}}+16}{{{x}^{2}}} \right)}^{2}} \right]\left[ {{\left( \frac{{{x}^{2}}+4}{x} \right)}^{2}}+{{\left( \frac{{{x}^{2}}+4}{2} \right)}^{2}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/57710018bddc8fb04e95206bbbe5cc21.png)

 καταλήγουμε στο να αναζητούμε
καταλήγουμε στο να αναζητούμε  ,
,  ,το οποίο επιτυγχάνεται για
,το οποίο επιτυγχάνεται για 
 ,
, 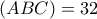
 και
και  , δηλαδή :
, δηλαδή :  και επιπλέον τα
και επιπλέον τα  είναι συνευθειακά .
είναι συνευθειακά . είναι απλή , ( το
είναι απλή , ( το  είναι το μέσο του
είναι το μέσο του  - σχετική εφαρμογή
- σχετική εφαρμογή  ,
,
Πράγματι ο λόγος των εμβαδών (ορθογωνίου τριγώνου προς παραβολικού χωρίου), για την γενικότερη παραβολή
 , ισούται προς
, ισούται προς 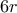 (βλέπετε διόρθωση του λόγου στην επόμενη δημοσίευση μου): αυτό προκύπτει από το προ ημερών αποτέλεσμα του Βασίλη και από το δικό μου αποτέλεσμα παρακάτω (στο οποίο έφτασα χωρίς να έχω δει την σημερινή ανάρτηση του Γιώργη):
(βλέπετε διόρθωση του λόγου στην επόμενη δημοσίευση μου): αυτό προκύπτει από το προ ημερών αποτέλεσμα του Βασίλη και από το δικό μου αποτέλεσμα παρακάτω (στο οποίο έφτασα χωρίς να έχω δει την σημερινή ανάρτηση του Γιώργη): τέμνει την παραβολή στο
τέμνει την παραβολή στο  , και οι εφαπτόμενες στα
, και οι εφαπτόμενες στα  ,
,  τέμνονται στο
τέμνονται στο  .
. ισούται προς
ισούται προς


 εύκολα βρίσκουμε ότι το εμβαδόν του
εύκολα βρίσκουμε ότι το εμβαδόν του  ελαχιστοποιείται για
ελαχιστοποιείται για  .
.Γνωστά πράγματα στον Αρχιμήδη. Αν η SK τεμνει την AB στο C , τότε, αφού είναι παράλληλη στον άξονα της παραβολής, το K είναι μέσο της SC και η (2) έπεται άμεσα.KARKAR έγραψε: ↑Κυρ Οκτ 15, 2017 12:44 pmΠαραβολικό χωρίο γ.pngΕίναι :και
, δηλαδή :
και επιπλέον τα
είναι συνευθειακά .
Η εύρεση τουείναι απλή , ( το
είναι το μέσο του
- σχετική εφαρμογή
υπάρχει στο σχολικό της Γ' Λυκείου ) . Δεν γνωρίζω αν υπάρχει απόδειξη του,
εικάζω πάντως ότι δεν είναι κάτι ιδιαίτερα δύσκολο
Σημείωση : Άξονας συμμετρίας της παραβολής θεωρήθηκε ο
Διορθώνω: ο λόγος του εμβαδού του ορθογωνίου τριγώνου προς το εμβαδόν του παραβολικού χωρίου ισούται όχι προςgbaloglou έγραψε: ↑Κυρ Οκτ 15, 2017 12:58 pmΠράγματι ο λόγος των εμβαδών (ορθογωνίου τριγώνου προς παραβολικού χωρίου), για την γενικότερη παραβολή, ισούται προς
: αυτό προκύπτει από το προ ημερών αποτέλεσμα του Βασίλη και από το δικό μου αποτέλεσμα παρακάτω (στο οποίο έφτασα χωρίς να έχω δει την σημερινή ανάρτηση του Γιώργη):
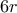 αλλά προς
αλλά προς 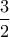 ... καθώς το πρώτο εμβαδόν ισούται προς
... καθώς το πρώτο εμβαδόν ισούται προς  (όπως προκύπτει από την σημερινή δημοσίευση του Γιώργη, αλλά και την δική μου) ενώ το δεύτερο εμβαδόν ισούται προς
(όπως προκύπτει από την σημερινή δημοσίευση του Γιώργη, αλλά και την δική μου) ενώ το δεύτερο εμβαδόν ισούται προς  .
. είναι η
είναι η  , οπότε ολοκληρώνοντας την
, οπότε ολοκληρώνοντας την  από
από  έως
έως  λαμβάνουμε
λαμβάνουμε  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης