Να βρεθεί η συνάρτηση
 αν ισχύει ότι:
αν ισχύει ότι:Συντονιστής: R BORIS
Καλησπέρα. Μια προσπάθεια...Tolaso J Kos έγραψε: ↑Κυρ Μάιος 20, 2018 1:51 pmΠαρόμοια κεντρική ιδέα ντυμένη αλλιώς...
Να βρεθεί η συνάρτησηαν ισχύει ότι:
 .
.

 .
. .
. προκύπτει
προκύπτει  . Άρα
. Άρα  .
. στο
στο ![[0,\frac{\pi}{2} ] [0,\frac{\pi}{2} ]](/forum/ext/geomar/texintegr/latexrender/pictures/bd06596d0bb659c487c0a74a059b9348.png) .
....κατ αρχάς πιστεύω ότι είναι ένα πολύ απαιτητικό θέμα και είναι λάθος ο φάκελλος που τοποθετήθηκε...Tolaso J Kos έγραψε: ↑Κυρ Μάιος 20, 2018 1:51 pmΠαρόμοια κεντρική ιδέα ντυμένη αλλιώς...
Να βρεθεί η συνάρτησηαν ισχύει ότι:
 γιατί
γιατί ![|f(x)|\ge 0,\,\,x\in [0,\,\frac{\pi }{2}] |f(x)|\ge 0,\,\,x\in [0,\,\frac{\pi }{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/74b156533fe58dd22fb77246ea91714c.png) έχουμε ότι
έχουμε ότι  επομένως
επομένως  και επειδή
και επειδή 
 επομένως
επομένως 
 και
και  και έχουμε τις περιπτώσεις
και έχουμε τις περιπτώσεις  τότε
τότε  που απορρίπτεται γιατί
που απορρίπτεται γιατί 
 τότε
τότε  και επειδή
και επειδή  σύμφωνα με το θεώρημα του Bolzano υπάρχει
σύμφωνα με το θεώρημα του Bolzano υπάρχει  ώστε
ώστε  και θα είναι η μοναδική ρίζα στο
και θα είναι η μοναδική ρίζα στο  γιατί αν υπάρχει και άλλη
γιατί αν υπάρχει και άλλη  με
με  σύμφωνα με το Rolle θα υπάρχει
σύμφωνα με το Rolle θα υπάρχει  που
που  άτοπο αφού
άτοπο αφού 
 επειδή
επειδή ![x\in [0,\frac{\pi }{2}] x\in [0,\frac{\pi }{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/7cd81c6e8fbd43195239a8dec969a46a.png) και
και  και ευκολότερα το πρόσημο…)
και ευκολότερα το πρόσημο…) θα έχει σταθερό πρόσημο στα
θα έχει σταθερό πρόσημο στα ![[0,\,{{x}_{0}}),\,({{x}_{2}}\,\,\frac{\pi }{2}] [0,\,{{x}_{0}}),\,({{x}_{2}}\,\,\frac{\pi }{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/56050d4c92820463dea8b3a5f60b85cb.png)
 ,
, θα είναι
θα είναι ![f(x)<0,\,\,x\in [0,\,{{x}_{0}}),\,f(x)>0,\,\,x\in ({{x}_{2}}\,\,\frac{\pi }{2}] f(x)<0,\,\,x\in [0,\,{{x}_{0}}),\,f(x)>0,\,\,x\in ({{x}_{2}}\,\,\frac{\pi }{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/808782253db515283058625ef6df5fae.png)



![\displaystyle \left[ \cos x+a\sin x \right]_{0}^{{{x}_{0}}}+\left[ -\cos x-a\sin x \right]_{0}^{{{x}_{0}}}=a\Leftrightarrow \displaystyle \left[ \cos x+a\sin x \right]_{0}^{{{x}_{0}}}+\left[ -\cos x-a\sin x \right]_{0}^{{{x}_{0}}}=a\Leftrightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/d500c88f13ac947825fcb55e1e983bf7.png)
![\displaystyle \left[ \cos x+a\sin x \right]_{0}^{{{x}_{0}}}+\left[ -\cos x-a\sin x \right]_{{{x}_{0}}}^{\frac{\pi }{2}}=a\Leftrightarrow \displaystyle \left[ \cos x+a\sin x \right]_{0}^{{{x}_{0}}}+\left[ -\cos x-a\sin x \right]_{{{x}_{0}}}^{\frac{\pi }{2}}=a\Leftrightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/c1fa85409e12554d92664c1345b0cba0.png)
![\displaystyle \begin{matrix}
& \left[ (\cos {{x}_{0}}+a\sin {{x}_{0}})-(cos0+a\sin 0) \right]- \\
& -\left[ (\cos \frac{\pi }{2}+a\sin \frac{\pi }{2})-(cos{{x}_{0}}+a\sin {{x}_{0}}) \right]=a\Leftrightarrow \\
\end{matrix} \displaystyle \begin{matrix}
& \left[ (\cos {{x}_{0}}+a\sin {{x}_{0}})-(cos0+a\sin 0) \right]- \\
& -\left[ (\cos \frac{\pi }{2}+a\sin \frac{\pi }{2})-(cos{{x}_{0}}+a\sin {{x}_{0}}) \right]=a\Leftrightarrow \\
\end{matrix}](/forum/ext/geomar/texintegr/latexrender/pictures/f3ae35bdf56cecda368a856cdd3432ce.png)

 θα έχουμε και ότι
θα έχουμε και ότι  και
και  οπότε
οπότε  και
και  με πρόσθεση κατά μέλη προκύπτει ότι
με πρόσθεση κατά μέλη προκύπτει ότι  επομένως τότε
επομένως τότε 
 ...
... με
με  όπως προηγούμενα
όπως προηγούμενα 
![\displaystyle \left[ \cos x+\frac{3}{4}\sin x \right]_{0}^{{{x}_{0}}}+\left[ -\cos x-\frac{3}{4}\sin x \right]_{{{x}_{0}}}^{\frac{\pi }{2}}=2(\cos {{x}_{0}}+\frac{3}{4}\sin {{x}_{0}})-\frac{7}{4} \displaystyle \left[ \cos x+\frac{3}{4}\sin x \right]_{0}^{{{x}_{0}}}+\left[ -\cos x-\frac{3}{4}\sin x \right]_{{{x}_{0}}}^{\frac{\pi }{2}}=2(\cos {{x}_{0}}+\frac{3}{4}\sin {{x}_{0}})-\frac{7}{4}](/forum/ext/geomar/texintegr/latexrender/pictures/2c0af286adb2d55034a9fda02de729f9.png)
 και επειδή
και επειδή 
 έτσι
έτσι 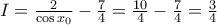
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες