Σελίδα 1 από 1
Ένα ορισμένο ολοκλήρωμα
Δημοσιεύτηκε: Δευ Μάιος 21, 2018 10:23 am
από Tolaso J Kos
Να δειχθεί ότι:
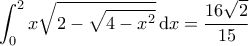
Re: Ένα ορισμένο ολοκλήρωμα
Δημοσιεύτηκε: Δευ Μάιος 21, 2018 7:11 pm
από Σταμ. Γλάρος
Tolaso J Kos έγραψε: ↑Δευ Μάιος 21, 2018 10:23 am
Να δειχθεί ότι:

Καλησπέρα. Μια προσπάθεια ...
Θέτω

. Είναι

, οπότε

.
Ξαναθέτω

. Είναι

, οπότε

.
Φιλικά
Σταμ. Γλάρος
Re: Ένα ορισμένο ολοκλήρωμα
Δημοσιεύτηκε: Δευ Μάιος 21, 2018 10:22 pm
από Mihalis_Lambrou
Tolaso J Kos έγραψε: ↑Δευ Μάιος 21, 2018 10:23 am
Να δειχθεί ότι:

Χάριν ποικιλίας και για όφελος των μαθητών, αλλιώς: Θέτουμε

οπότε


. Το ολοκλήρωμα γίνεται

που είναι απλό (γνωστό/βασικό).
Edit: Διόρθωσα λογιστική μικροαπροσεξία.
Re: Ένα ορισμένο ολοκλήρωμα
Δημοσιεύτηκε: Τρί Μάιος 22, 2018 2:12 am
από Christos.N
Ας δούμε την συνέχεια τότε.
Re: Ένα ορισμένο ολοκλήρωμα
Δημοσιεύτηκε: Τρί Μάιος 22, 2018 7:04 am
από Mihalis_Lambrou
Christos.N έγραψε: ↑Τρί Μάιος 22, 2018 2:12 am
Ας δούμε την συνέχεια τότε.
.
Υπόδειξη:

Ας σημειώσω ότι πρόκειται για στάνταρ τεχνική που μπορεί κανείς να την
βρει σε όλα τα βιβλία με τεχνικές ολοκλήρωσης.
Re: Ένα ορισμένο ολοκλήρωμα
Δημοσιεύτηκε: Τρί Μάιος 22, 2018 11:45 am
από Tolaso J Kos
Mihalis_Lambrou έγραψε: ↑Δευ Μάιος 21, 2018 10:22 pm
Tolaso J Kos έγραψε: ↑Δευ Μάιος 21, 2018 10:23 am
Να δειχθεί ότι:

Χάριν ποικιλίας και για όφελος των μαθητών, αλλιώς: Θέτουμε

οπότε


. Το ολοκλήρωμα γίνεται
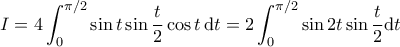
που είναι απλό (γνωστό/βασικό).
Γεια σας κ. Μιχάλη. Κάπου πρέπει να σας έχει ξεφύγει ένα δυάρι γιατί αυτό που βγάζετε δεν ταιριάζει αριθμητικά.
Re: Ένα ορισμένο ολοκλήρωμα
Δημοσιεύτηκε: Τετ Μάιος 23, 2018 10:35 am
από Mihalis_Lambrou
Tolaso J Kos έγραψε: ↑Τρί Μάιος 22, 2018 11:45 am
Κάπου πρέπει να σας έχει ξεφύγει ένα δυάρι γιατί αυτό που βγάζετε δεν ταιριάζει αριθμητικά.
Τόλη, έχεις δίκιο. Το διόρθωσα.
Τώρα είδα το μήνυμά σου καθώς ταξιδεύω για το εξωτερικό (συνέδριο Ιστορίας των Μαθηματικών, στην Ουγγαρία).
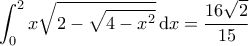
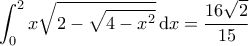
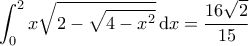
 . Είναι
. Είναι  , οπότε
, οπότε  .
. . Είναι
. Είναι  , οπότε
, οπότε  .
. οπότε
οπότε 
 . Το ολοκλήρωμα γίνεται
. Το ολοκλήρωμα γίνεται 

οπότε
. Το ολοκλήρωμα γίνεται