Να λυθεί η εξίσωση:

Συντονιστής: R BORIS

Το αόριστο ολοκλήρωμα δίνει (άμεσο και γνωστό)
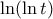 . Άρα η εξίσωση είναι
. Άρα η εξίσωση είναι  . Προφανής ρίζα η
. Προφανής ρίζα η  . Είναι και μοναδική διότι το αριστερό μέλος είναι γνήσια αύξουσα συνάρτηση και το δεξί γνήσια φθίνουσα.
. Είναι και μοναδική διότι το αριστερό μέλος είναι γνήσια αύξουσα συνάρτηση και το δεξί γνήσια φθίνουσα.Δεύτερες σκέψεις, καλύτερες: Δεν χρειάζεται να ολοκληρώσουμε!Mihalis_Lambrou έγραψε: ↑Τετ Ιαν 16, 2019 12:33 pmΤο αόριστο ολοκλήρωμα δίνει (άμεσο και γνωστό). Άρα η εξίσωση είναι
. Προφανής ρίζα η
. Είναι και μοναδική διότι το αριστερό μέλος είναι γνήσια αύξουσα συνάρτηση και το δεξί γνήσια φθίνουσα.
 , σημαίνει ότι το αριστερό μέλος είναι γνήσια αύξουσα συνάρτηση. Προφανής ρίζα η
, σημαίνει ότι το αριστερό μέλος είναι γνήσια αύξουσα συνάρτηση. Προφανής ρίζα η  (και τα δύο μέλη ίσα με
(και τα δύο μέλη ίσα με  ). Είναι μοναδική αφού, όπως πριν, το το δεξί μέλος είναι γνήσια φθίνουσα συνάρτηση.
). Είναι μοναδική αφού, όπως πριν, το το δεξί μέλος είναι γνήσια φθίνουσα συνάρτηση. ) γιατί το αντίστοιχο αόριστο ολοκλήρωμα δίνει
) γιατί το αντίστοιχο αόριστο ολοκλήρωμα δίνει 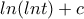 και όχι
και όχι  ; Ακόμη, στη δεύτερη λύση σας, βασίζεστε στο πεδίο ορισμού της
; Ακόμη, στη δεύτερη λύση σας, βασίζεστε στο πεδίο ορισμού της  για να πείτε ότι
για να πείτε ότι  , γιατί αλλιώς πως προκύπτει κάτι τέτοιο; Ευχαριστώ και πάλι θερμά.
, γιατί αλλιώς πως προκύπτει κάτι τέτοιο; Ευχαριστώ και πάλι θερμά.Μυρτώ, Καλή Χρονιά.pito έγραψε: ↑Τετ Ιαν 16, 2019 1:45 pmκ.Λάμπρου, καλή χρονιά! Σας ευχαριστώ για την ενασχόληση σας.Σε κάποια σημεία της λύσης σας έχω απορίες. Αν δεν βασιστούμε στο πεδίο ορισμού της συνάρτησης ολοκλήρωμα (που είναι το) γιατί το αντίστοιχο αόριστο ολοκλήρωμα δίνει
και όχι
; Ακόμη, στη δεύτερη λύση σας, βασίζεστε στο πεδίο ορισμού της
για να πείτε ότι
, γιατί αλλιώς πως προκύπτει κάτι τέτοιο; Ευχαριστώ και πάλι θερμά.
 αλλά όταν ολοκληρώνουμε σε διάστημα
αλλά όταν ολοκληρώνουμε σε διάστημα ![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) πρέπει, λόγω της ασυνέχειας στο
πρέπει, λόγω της ασυνέχειας στο  , να εργαστούμε με περιορισμό είτε
, να εργαστούμε με περιορισμό είτε ![[a,b] \subseteq (0, 1) [a,b] \subseteq (0, 1)](/forum/ext/geomar/texintegr/latexrender/pictures/99bd22c1661611bfc451ae13fb9687eb.png) ή
ή ![[a,b] \subseteq (1,\infty) [a,b] \subseteq (1,\infty)](/forum/ext/geomar/texintegr/latexrender/pictures/b45e23cf8c2e71e40927ac5116b4941d.png) . Συνηθίζουμε το δεύτερο, γι' αυτό άλλωστε λέμε (όπως έγραψες) ότι το π.ο. είναι το
. Συνηθίζουμε το δεύτερο, γι' αυτό άλλωστε λέμε (όπως έγραψες) ότι το π.ο. είναι το  . Και αυτό έκανα στις λύσεις μου (βλέπε παρακάτω για την αιτία).
. Και αυτό έκανα στις λύσεις μου (βλέπε παρακάτω για την αιτία).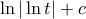 . Επειδή όμως μας ενδιαφέρει η συνάρτηση να ορίζεται στο
. Επειδή όμως μας ενδιαφέρει η συνάρτηση να ορίζεται στο  (που είναι άκρο του δοθέντος ολοκληρώματος) είναι σαφές ότι εργαζόμαστε στο
(που είναι άκρο του δοθέντος ολοκληρώματος) είναι σαφές ότι εργαζόμαστε στο  . Εκεί η προς ολοκλήρωση συνάρτηση είναι για προφανείς λόγους
. Εκεί η προς ολοκλήρωση συνάρτηση είναι για προφανείς λόγους  , οπότε το απόλυτο στην απάντηση περιττεύει. Σε αυτό βασίστηκα και στην δεύτερη λύση όταν γράφω ότι "το μέσα είναι
, οπότε το απόλυτο στην απάντηση περιττεύει. Σε αυτό βασίστηκα και στην δεύτερη λύση όταν γράφω ότι "το μέσα είναι  ". Το θεώρησα προφανές.
". Το θεώρησα προφανές.  . Και λοιπά.
. Και λοιπά. . 'Εχουμε:
. 'Εχουμε: 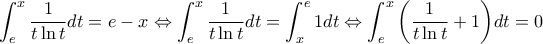 . Όμως, ισχύει:
. Όμως, ισχύει:  ,
,  . Οπότε, είναι:
. Οπότε, είναι:  , αν
, αν  και
και 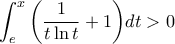 , αν
, αν  . Άρα, μοναδική λύση της εξίσωσης είναι η
. Άρα, μοναδική λύση της εξίσωσης είναι η  , που πράγματι την επαληθεύει, αφού
, που πράγματι την επαληθεύει, αφού  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες