Mihalis_Lambrou έγραψε: ↑Παρ Δεκ 27, 2019 11:26 pmΆσκηση 33
Να υπολογισθεί το ολοκλήρωμα
(Αρκετά απλή. Την βάζω εδώ μόνο και μόνο επειδή με πρώτη ματιά τρομάζει.)

Χρησιμοποιώντας διαδοχικά τους μετασχηματισμούς
 έχω:
έχω: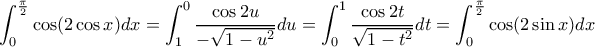
Άρα,

Συντονιστής: R BORIS
Mihalis_Lambrou έγραψε: ↑Παρ Δεκ 27, 2019 11:26 pmΆσκηση 33
Να υπολογισθεί το ολοκλήρωμα
(Αρκετά απλή. Την βάζω εδώ μόνο και μόνο επειδή με πρώτη ματιά τρομάζει.)

 έχω:
έχω: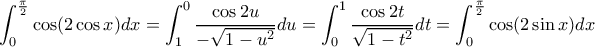

Διαφορετικά με αλλαγή μεταβλητήςMihalis_Lambrou έγραψε: ↑Παρ Δεκ 27, 2019 11:26 pmΆσκηση 33
Να υπολογισθεί το ολοκλήρωμα
(Αρκετά απλή. Την βάζω εδώ μόνο και μόνο επειδή με πρώτη ματιά τρομάζει.)
 το ολοκλήρωμα γίνεται:
το ολοκλήρωμα γίνεται:


Με τον μετασχηματισμό
 και με διαδοχικές παραγοντικές ολοκληρώσεις καταλήγω στο
και με διαδοχικές παραγοντικές ολοκληρώσεις καταλήγω στο![\displaystyle \int_0^k {\frac{{\sqrt x }}{{{e^{\sqrt x }}}}} dx = \left[ { - 2{u^2}{e^{ - u}} - 4u{e^{ - u}} - 4{e^{ - u}}} \right]_0^{\sqrt k } = 4 - \frac{{2k + 4\sqrt k + 4}}{{{e^{\sqrt k }}}} > 3 \Leftrightarrow \displaystyle \int_0^k {\frac{{\sqrt x }}{{{e^{\sqrt x }}}}} dx = \left[ { - 2{u^2}{e^{ - u}} - 4u{e^{ - u}} - 4{e^{ - u}}} \right]_0^{\sqrt k } = 4 - \frac{{2k + 4\sqrt k + 4}}{{{e^{\sqrt k }}}} > 3 \Leftrightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/36a210cd8011776f5e7160594854fcb1.png)
 όπου με τη βοήθεια λογισμικού βρίσκω
όπου με τη βοήθεια λογισμικού βρίσκω  άρα η απάντηση είναι
άρα η απάντηση είναι 


Υπολογίζω πρώτα το αόριστο ολοκλήρωμα μεTolaso J Kos έγραψε: ↑Σάβ Δεκ 28, 2019 1:05 pmΆσκηση 35
Να υπολογιστεί το ολοκλήρωμα:

Αντιμετωπίζεται εύκολα χωρίς τριγωνομετρικά!



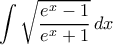
 του οποίου θα χρειαστείτε μία παραλλαγή).
του οποίου θα χρειαστείτε μία παραλλαγή).Δεν καταλαβαίνω τι θα πει με Λογισμικό.george visvikis έγραψε: ↑Σάβ Δεκ 28, 2019 1:04 pmΜε τον μετασχηματισμόκαι με διαδοχικές παραγοντικές ολοκληρώσεις καταλήγω στο
όπου με τη βοήθεια λογισμικού βρίσκω
άρα η απάντηση είναι

ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Κυρ Δεκ 29, 2019 1:34 amΔεν καταλαβαίνω τι θα πει με Λογισμικό.george visvikis έγραψε: ↑Σάβ Δεκ 28, 2019 1:04 pmΜε τον μετασχηματισμόκαι με διαδοχικές παραγοντικές ολοκληρώσεις καταλήγω στο
όπου με τη βοήθεια λογισμικού βρίσκω
άρα η απάντηση είναι

Με λογισμικό πολλά από τα θέματα στο
είναι άνευ σημασίας.
Και σε κάθε περίπτωση το Λογισμικό είναι καθαρά υποκειμενικό.
Ο τερματισμός από ότι βλέπω είναι γενικός.
Δεν έχω κανένα πρόβλημα με τα Λογισμικά.
Ισα ίσα αυτά είναι το μέλλον.
Αλλά ότι γράφεται θα πρέπει θα πρέπει να έχει απάντηση χωρίς Λογισμικό.
Ασχετα ότι κάποιοι θα ''κλέβουν'' με τα Λογισμικά.
 χωρίς λογισμικό.
χωρίς λογισμικό.

 αφού
αφού  . Οπότε θέτοντας
. Οπότε θέτοντας  έχουμε
έχουμε  .
. έβαλα
έβαλα  .
.![f:[0,1]\longrightarrow \mathbb R f:[0,1]\longrightarrow \mathbb R](/forum/ext/geomar/texintegr/latexrender/pictures/90873e64faeeaae808ffc3c1dd91d3ae.png) συνάρτηση που για κάθε
συνάρτηση που για κάθε ![x\in [0,1] x\in [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/c628ba2b1047de93f66cb815d986e107.png) ικανοποιεί
ικανοποιεί  .
.  .
. μένει αναπάντητη. )
μένει αναπάντητη. )ΘέτωMihalis_Lambrou έγραψε: ↑Σάβ Δεκ 28, 2019 10:43 pmΆσκηση 37
Να υπολογισθεί το ολοκλήρωμα
(Μπορείτε να θεωρήσετε γνωστό τοτου οποίου θα χρειαστείτε μία παραλλαγή).
 και
και  άρα το ολοκλήρωμα γράφεται:
άρα το ολοκλήρωμα γράφεται:
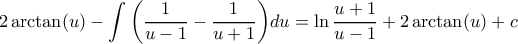
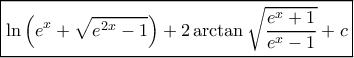
Λίγο αλλιώς. Γράφω λύση γιατί οδηγεί σεgeorge visvikis έγραψε: ↑Κυρ Δεκ 29, 2019 5:33 pmΘέτωMihalis_Lambrou έγραψε: ↑Σάβ Δεκ 28, 2019 10:43 pmΆσκηση 37
Να υπολογισθεί το ολοκλήρωμα
(Μπορείτε να θεωρήσετε γνωστό τοτου οποίου θα χρειαστείτε μία παραλλαγή).
και
άρα το ολοκλήρωμα γράφεται:
Τα υπόλοιπα είναι αντικατάσταση με τελικό αποτέλεσμα
 αντί
αντί  της λύσης του Γιώργου.
της λύσης του Γιώργου.  οπότε το ολοκλήρωμα γίνεται
οπότε το ολοκλήρωμα γίνεται 
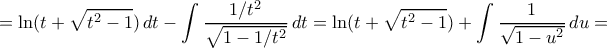


 για
για  .
. . Προσοχή όμως, οδηγεί σε
. Προσοχή όμως, οδηγεί σε 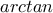 , αλλά σε μορφή που το είδαμε εδώ πολλές φορές).
, αλλά σε μορφή που το είδαμε εδώ πολλές φορές)..Mihalis_Lambrou έγραψε: ↑Κυρ Δεκ 29, 2019 3:25 pmΆσκηση 39
Έστωσυνάρτηση που για κάθε
ικανοποιεί
.
Να υπολογισθεί το ολοκλήρωμα.
 και ολοκληρώστε.
και ολοκληρώστε.Καλημέρα και χρόνια πολλάMihalis_Lambrou έγραψε: ↑Πέμ Ιαν 02, 2020 1:14 pm.Mihalis_Lambrou έγραψε: ↑Κυρ Δεκ 29, 2019 3:25 pmΆσκηση 39
Έστωσυνάρτηση που για κάθε
ικανοποιεί
.
Να υπολογισθεί το ολοκλήρωμα.
Υπόδειξη: Πολλαπλασιάστε την δοθείσα επίκαι ολοκληρώστε.


 .
.  . Θέτω
. Θέτω  .
.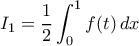 .
. . Θέτω
. Θέτω  .
. .
. .
. από όπου έχουμε
από όπου έχουμε  .
.
 , ώστε :
, ώστε : 
i)
 .
. είναι
είναι  και για
και για  είναι
είναι 
 (απόδειξη απλή αλλά εκτός ύλης), πλην όμως το ολοκλήρωμα υπολογίζεται ούτως ή άλλως στοιχειωδώς, οπότε δεν έχουμε πρόβλημα. Το αόριστο ισούται
(απόδειξη απλή αλλά εκτός ύλης), πλην όμως το ολοκλήρωμα υπολογίζεται ούτως ή άλλως στοιχειωδώς, οπότε δεν έχουμε πρόβλημα. Το αόριστο ισούται  .
.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες