 με
με 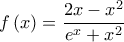 .
.α) Να βρεθεί το εμβαδόν,
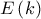 , του χωρίου που περικλείεται από τη γραφική
, του χωρίου που περικλείεται από τη γραφική παράσταση της
 , τον άξονα
, τον άξονα  και τις ευθείες με εξισώσεις :
και τις ευθείες με εξισώσεις : 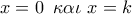 με
με 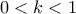 .
. β) Να βρεθεί το όριο
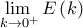 .
.Συντονιστής: R BORIS
 με
με 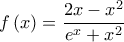 .
.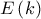 , του χωρίου που περικλείεται από τη γραφική
, του χωρίου που περικλείεται από τη γραφική  , τον άξονα
, τον άξονα  και τις ευθείες με εξισώσεις :
και τις ευθείες με εξισώσεις : 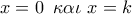 με
με 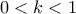 .
. 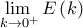 .
.Γεια σου Νίκο,
 στο εν λόγω διάστημα το εμβαδόν δίδεται του τύπου:
στο εν λόγω διάστημα το εμβαδόν δίδεται του τύπου:![\displaystyle{\begin{aligned}
\mathrm{E} \left ( \kappa \right ) &= \int_{0}^{\kappa} f(x)\, \mathrm{d}x \\
&= \int_{0}^{\kappa} \frac{2x-x^2}{e^x+x^2}\, \mathrm{d}x \\
&= \int_{0}^{\kappa} \frac{e^x +2x - e^x-x^2}{e^x+x^2}\, \mathrm{d}x \\
&= \int_{0}^{\kappa} \left ( \frac{e^x+2x}{e^x+x^2} - \frac{e^x+x^2}{e^x+x^2} \right )\,\mathrm{d}x \\
&= \int_{0}^{\kappa} \frac{\left ( e^x + x^2 \right )'}{e^x+x^2}\, \mathrm{d}x - \int_{0}^{\kappa} \, \mathrm{d}x \\
&= \left [ \ln \left ( e^x + x^2 \right ) \right ]_0^\kappa - \left ( \kappa -0 \right ) \\
&= \ln \left ( e^\kappa + \kappa^2 \right ) - \kappa \\
&= \ln \left ( e^\kappa + \kappa^2 \right ) - \ln e^\kappa \\
&= \ln \frac{e^\kappa + \kappa^2}{e^\kappa} \\
&= \ln \left ( 1 + \kappa^2 e^{-\kappa} \right )
\end{aligned}} \displaystyle{\begin{aligned}
\mathrm{E} \left ( \kappa \right ) &= \int_{0}^{\kappa} f(x)\, \mathrm{d}x \\
&= \int_{0}^{\kappa} \frac{2x-x^2}{e^x+x^2}\, \mathrm{d}x \\
&= \int_{0}^{\kappa} \frac{e^x +2x - e^x-x^2}{e^x+x^2}\, \mathrm{d}x \\
&= \int_{0}^{\kappa} \left ( \frac{e^x+2x}{e^x+x^2} - \frac{e^x+x^2}{e^x+x^2} \right )\,\mathrm{d}x \\
&= \int_{0}^{\kappa} \frac{\left ( e^x + x^2 \right )'}{e^x+x^2}\, \mathrm{d}x - \int_{0}^{\kappa} \, \mathrm{d}x \\
&= \left [ \ln \left ( e^x + x^2 \right ) \right ]_0^\kappa - \left ( \kappa -0 \right ) \\
&= \ln \left ( e^\kappa + \kappa^2 \right ) - \kappa \\
&= \ln \left ( e^\kappa + \kappa^2 \right ) - \ln e^\kappa \\
&= \ln \frac{e^\kappa + \kappa^2}{e^\kappa} \\
&= \ln \left ( 1 + \kappa^2 e^{-\kappa} \right )
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/7875537c6aa139f4bebb2443f38969bc.png)
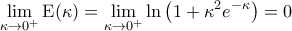 .
.
Tolaso J Kos έγραψε: ↑Δευ Μάιος 29, 2023 2:12 pmΓεια σου Νίκο,
(α) Επειδήστο εν λόγω διάστημα το εμβαδόν δίδεται του τύπου:
![\displaystyle{\begin{aligned}
\mathrm{E} \left ( \kappa \right ) &= \int_{0}^{\kappa} f(x)\, \mathrm{d}x \\
&= \int_{0}^{\kappa} \frac{2x-x^2}{e^x+x^2}\, \mathrm{d}x \\
&= \int_{0}^{\kappa} \frac{e^x +2x - e^x-x^2}{e^x+x^2}\, \mathrm{d}x \\
&= \int_{0}^{\kappa} \left ( \frac{e^x+2x}{e^x+x^2} - \frac{e^x+x^2}{e^x+x^2} \right )\,\mathrm{d}x \\
&= \int_{0}^{\kappa} \frac{\left ( e^x + x^2 \right )'}{e^x+x^2}\, \mathrm{d}x - \int_{0}^{\kappa} \, \mathrm{d}x \\
&= \left [ \ln \left ( e^x + x^2 \right ) \right ]_0^\kappa - \left ( \kappa -0 \right ) \\
&= \ln \left ( e^\kappa + \kappa^2 \right ) - \kappa \\
&= \ln \left ( e^\kappa + \kappa^2 \right ) - \ln e^\kappa \\
&= \ln \frac{e^\kappa + \kappa}{e^\kappa} \\
&= \ln \left ( 1 + \kappa e^{-\kappa} \right )
\end{aligned}} \displaystyle{\begin{aligned}
\mathrm{E} \left ( \kappa \right ) &= \int_{0}^{\kappa} f(x)\, \mathrm{d}x \\
&= \int_{0}^{\kappa} \frac{2x-x^2}{e^x+x^2}\, \mathrm{d}x \\
&= \int_{0}^{\kappa} \frac{e^x +2x - e^x-x^2}{e^x+x^2}\, \mathrm{d}x \\
&= \int_{0}^{\kappa} \left ( \frac{e^x+2x}{e^x+x^2} - \frac{e^x+x^2}{e^x+x^2} \right )\,\mathrm{d}x \\
&= \int_{0}^{\kappa} \frac{\left ( e^x + x^2 \right )'}{e^x+x^2}\, \mathrm{d}x - \int_{0}^{\kappa} \, \mathrm{d}x \\
&= \left [ \ln \left ( e^x + x^2 \right ) \right ]_0^\kappa - \left ( \kappa -0 \right ) \\
&= \ln \left ( e^\kappa + \kappa^2 \right ) - \kappa \\
&= \ln \left ( e^\kappa + \kappa^2 \right ) - \ln e^\kappa \\
&= \ln \frac{e^\kappa + \kappa}{e^\kappa} \\
&= \ln \left ( 1 + \kappa e^{-\kappa} \right )
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/d987abfe074e458134fd0ecd66b732bd.png)
(β) Είναι.
Τόλη, παρόλο που είναι εύκολη η άσκηση, την έχεις γράψει τόσο καθαρογραμμένα που η λύση σου εντυπωσιάζει !!Tolaso J Kos έγραψε: ↑Δευ Μάιος 29, 2023 2:12 pmΓεια σου Νίκο,
(α) Επειδήστο εν λόγω διάστημα το εμβαδόν δίδεται του τύπου:
![\displaystyle{\begin{aligned}
\mathrm{E} \left ( \kappa \right ) &= \int_{0}^{\kappa} f(x)\, \mathrm{d}x \\
&= \int_{0}^{\kappa} \frac{2x-x^2}{e^x+x^2}\, \mathrm{d}x \\
&= \int_{0}^{\kappa} \frac{e^x +2x - e^x-x^2}{e^x+x^2}\, \mathrm{d}x \\
&= \int_{0}^{\kappa} \left ( \frac{e^x+2x}{e^x+x^2} - \frac{e^x+x^2}{e^x+x^2} \right )\,\mathrm{d}x \\
&= \int_{0}^{\kappa} \frac{\left ( e^x + x^2 \right )'}{e^x+x^2}\, \mathrm{d}x - \int_{0}^{\kappa} \, \mathrm{d}x \\
&= \left [ \ln \left ( e^x + x^2 \right ) \right ]_0^\kappa - \left ( \kappa -0 \right ) \\
&= \ln \left ( e^\kappa + \kappa^2 \right ) - \kappa \\
&= \ln \left ( e^\kappa + \kappa^2 \right ) - \ln e^\kappa \\
&= \ln \frac{e^\kappa + \kappa}{e^\kappa} \\
&= \ln \left ( 1 + \kappa e^{-\kappa} \right )
\end{aligned}} \displaystyle{\begin{aligned}
\mathrm{E} \left ( \kappa \right ) &= \int_{0}^{\kappa} f(x)\, \mathrm{d}x \\
&= \int_{0}^{\kappa} \frac{2x-x^2}{e^x+x^2}\, \mathrm{d}x \\
&= \int_{0}^{\kappa} \frac{e^x +2x - e^x-x^2}{e^x+x^2}\, \mathrm{d}x \\
&= \int_{0}^{\kappa} \left ( \frac{e^x+2x}{e^x+x^2} - \frac{e^x+x^2}{e^x+x^2} \right )\,\mathrm{d}x \\
&= \int_{0}^{\kappa} \frac{\left ( e^x + x^2 \right )'}{e^x+x^2}\, \mathrm{d}x - \int_{0}^{\kappa} \, \mathrm{d}x \\
&= \left [ \ln \left ( e^x + x^2 \right ) \right ]_0^\kappa - \left ( \kappa -0 \right ) \\
&= \ln \left ( e^\kappa + \kappa^2 \right ) - \kappa \\
&= \ln \left ( e^\kappa + \kappa^2 \right ) - \ln e^\kappa \\
&= \ln \frac{e^\kappa + \kappa}{e^\kappa} \\
&= \ln \left ( 1 + \kappa e^{-\kappa} \right )
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/d987abfe074e458134fd0ecd66b732bd.png)
(β) Είναι.
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες