A. Θεωρούμε την συνάρτηση
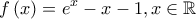 η οπόια είναι συνεχής και παραγωγίσιμη με πρώτη παράγωγο
η οπόια είναι συνεχής και παραγωγίσιμη με πρώτη παράγωγο . Εύκολα βλέπουμε
. Εύκολα βλέπουμε  .
.Για
 οπότε στο
οπότε στο 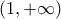 η συναρτηση ειναι γνησιως αυξουσα.
η συναρτηση ειναι γνησιως αυξουσα.Για
 οπότε στο
οπότε στο  η συναρτηση ειναι γνησιως φθινουσα.
η συναρτηση ειναι γνησιως φθινουσα.Άρα παρουσιαζει η συναρτηση ακροτατο στο
 το οποίο στην περιπτωσή μας είναι ολικό άρα
το οποίο στην περιπτωσή μας είναι ολικό άρα  .
.Η ισότητα λαμβανεται όταν
 .
.2. Άν στην πάνω ανισότητα βάλω όπου
 το
το 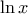 άρα θα λαβουμε:
άρα θα λαβουμε:  .
.Άρα

Όμοια λαμβανω

Πολλαπλασιαζοντας τις κατα μελη μιας και τα μάλη τους είναι θετικα θα λάβω:
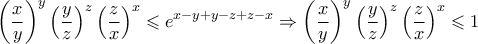
Η ισότητα λαμβανεται όταν
 ( ουσιαστικα προκύπτει όταν λαμβανεται στις
( ουσιαστικα προκύπτει όταν λαμβανεται στις  όταν
όταν 
όμοια και για τις αλλες δυο).
 Απέδειξα την
Απέδειξα την 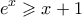 για το αλλο ερώτημα.
για το αλλο ερώτημα.Η
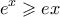 όμως η πάνω δηλαδη θεωρούμε τη συναρτηση
όμως η πάνω δηλαδη θεωρούμε τη συναρτηση 
και
 . Επειδή ειναι γνησίως αύξουσα στο
. Επειδή ειναι γνησίως αύξουσα στο 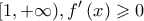
και γνησίως φθίνουσα στο
![\displaystyle (-\infty,1],f'\left(x \right)\leqslant 0 \displaystyle (-\infty,1],f'\left(x \right)\leqslant 0](/forum/ext/geomar/texintegr/latexrender/pictures/cace95a92966e8aa08d9953c9d48b3b6.png) . Άρα στο
. Άρα στο  παρουσιαζει ακροτατο το οπίο είναι ολικό το
παρουσιαζει ακροτατο το οπίο είναι ολικό το .
.
 για κάθε
για κάθε  ,
,  .
.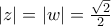 με
με  ,
,  , για την οποία ισχύει:
, για την οποία ισχύει:  για κάθε
για κάθε  .
.  έχει τουλάχιστον μια ρίζα
έχει τουλάχιστον μια ρίζα  .
.


![\displaystyle{{\left[ {f\left( {f\left( x \right)} \right)} \right]^2} = {\left| {z + xw} \right|^2} = \left( {z + xw} \right)\left( {\bar z + x\bar w} \right) = z\bar z + {x^2}w\bar w + xw\bar z + xz\bar w = } \displaystyle{{\left[ {f\left( {f\left( x \right)} \right)} \right]^2} = {\left| {z + xw} \right|^2} = \left( {z + xw} \right)\left( {\bar z + x\bar w} \right) = z\bar z + {x^2}w\bar w + xw\bar z + xz\bar w = }](/forum/ext/geomar/texintegr/latexrender/pictures/d395266dd50dfd71341abce16f37e867.png)



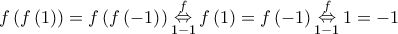

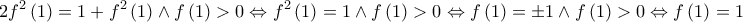

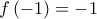 τότε
τότε  άτοπο, άρα
άτοπο, άρα 
![\displaystyle{g\left( x \right) = f\left( x \right) - 2x,x \in \left[ { - 1,1} \right]} \displaystyle{g\left( x \right) = f\left( x \right) - 2x,x \in \left[ { - 1,1} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/80abaca43d6b2a3920c10baffb80cb09.png)
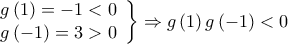



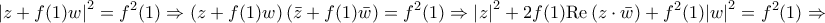
 .
.  .
. ,
,  για την οποία γνωρίζουμε ότι ισχύουν:
για την οποία γνωρίζουμε ότι ισχύουν:  και
και  ,
, ,
,  για τους οποίους γνωρίζουμε ότι ισχύουν:
για τους οποίους γνωρίζουμε ότι ισχύουν: 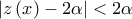 ,
,  και
και  για κάθε
για κάθε  .
.
 (1)
(1)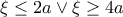
 (2)
(2) καθώς και στη γραφική παράσταση της συνάρτησης f και που βρίσκεται ταυτόχρονα στον άξονα
καθώς και στη γραφική παράσταση της συνάρτησης f και που βρίσκεται ταυτόχρονα στον άξονα  είναι το
είναι το  .
. με
με  , επομένως
, επομένως  και τελικά
και τελικά  .
. gatisies!!
gatisies!! 
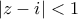 ,
, 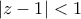 ,
,  ,
,  ,
,  :
: ,
,  .
. 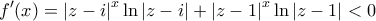 η f γν.φθίνουσα για κάθε
η f γν.φθίνουσα για κάθε  άρα η x=0 είναι και μοναδική
άρα η x=0 είναι και μοναδική και το
και το 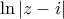 είναι αρνητικά καθώς η ποσότητες που είναι μέσα στο ln ειναι μικρότερες της μονάδας
είναι αρνητικά καθώς η ποσότητες που είναι μέσα στο ln ειναι μικρότερες της μονάδας ο γ.τ. είναι τα εσωτερικά σημεία του κύκλου με κέντρο Κ(0,1) και ακτίνα 1
ο γ.τ. είναι τα εσωτερικά σημεία του κύκλου με κέντρο Κ(0,1) και ακτίνα 1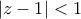 ο γ.τ. είναι τα εσωτερικά σημεία του κύκλου με κέντρο Λ(1,0) και ακτίνα 1
ο γ.τ. είναι τα εσωτερικά σημεία του κύκλου με κέντρο Λ(1,0) και ακτίνα 1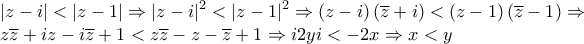
 με
με  άρα
άρα 
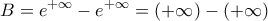 απροσδιοριστία
απροσδιοριστία τότε
τότε 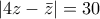


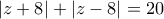 , επομένως οι εικόνες των z βρίσκονται στην έλλειψη με εξίσωση:
, επομένως οι εικόνες των z βρίσκονται στην έλλειψη με εξίσωση: .
.