Έστω συνάρτηση
ώστε να ισχύει 
για κάθε 
.i. Να δείξετε ότι η
είναι περιττή.ii. Να δείξετε ότι
για κάθε 
iii. Να δείξετε ότι η
είναι γνησίως αύξουσα στο 
.iv. Να υπολογίσετε τα όρια
, 
.v. Να δείξετε ότι η
είναι συνεχής στο vi. Να βρείτε το σύνολο τιμών
vii. Να δείξετε ότι η
είναι παραγωγίσιμη στο viii. Να δικαιολογήσετε την αντιστρεψιμότητα της
και να βρείτε το είδος της μονοτονίας της αντίστροφηςix. Να βρείτε τον τύπο της
.x. Να λύσετε την εξίσωση
xi. Να δείξετε ότι η
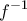είναι συνεχής στο .xii. Να βρείτε τον τύπο της
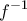
xiii. Να βρεθεί, αν υπάρχει το
xiv. Να υπολογίσετε το ολοκλήρωμα
![\displaystyle{I = \int\limits_0^{\sqrt[3]{{10}}} {\left( {12x\int\limits_{\sqrt[3]{{10}}}^x {\frac{{f\left( t \right)}}{{3{f^2}\left( t \right) + 1}}dt} } \right)dx} }](/forum/ext/geomar/texintegr/latexrender/pictures/5b1f3896b657e269a23b43230b879757.png "\displaystyle{I = \int\limits_0^{\sqrt[3]{{10}}} {\left( {12x\int\limits_{\sqrt[3]{{10}}}^x {\frac{{f\left( t \right)}}{{3{f^2}\left( t \right) + 1}}dt} } \right)dx} }")
ΠΡΟΣΘΗΚΗ: Άλλαξα ένα υπολογίσετε σε βρείτε και έβαλα το σύνολο που ζητείται η παραγωγισιμότητα (παράλειψη)
το 
και βάζοντας όπου x το -x στην (1) έχουμε:
έχει αρνητική διακρίνουσα αν την θεωρήσουμε σαν τριώνυμο του f(x)
με 
ώστε:
άρα η 
γνησίως αύξουσα στο 
![{f^3}\left( x \right) + f\left( x \right) = {x^3} \Rightarrow {\left( {\frac{{f\left( x \right)}}{x}} \right)^3} + \frac{{f\left( x \right)}}{{{x^3}}} = 1 \Rightarrow \frac{{f\left( x \right)}}{x} = \sqrt[3]{{1 - \frac{{f\left( x \right)}}{{{x^3}}}}}](/forum/ext/geomar/texintegr/latexrender/pictures/ebec35934a66caab4173d05825d4ec53.png "{f^3}\left( x \right) + f\left( x \right) = {x^3} \Rightarrow {\left( {\frac{{f\left( x \right)}}{x}} \right)^3} + \frac{{f\left( x \right)}}{{{x^3}}} = 1 \Rightarrow \frac{{f\left( x \right)}}{x} = \sqrt[3]{{1 - \frac{{f\left( x \right)}}{{{x^3}}}}}")
![\mathop {\lim }\limits_{x \to + \infty } \frac{{f\left( x \right)}}{x} = \mathop {\lim }\limits_{x \to + \infty } \sqrt[3]{{1 - \frac{{f\left( x \right)}}{{{x^3}}}}} = 1](/forum/ext/geomar/texintegr/latexrender/pictures/d637a1fa743d5a800e66788a78c8ee5c.png "\mathop {\lim }\limits_{x \to + \infty } \frac{{f\left( x \right)}}{x} = \mathop {\lim }\limits_{x \to + \infty } \sqrt[3]{{1 - \frac{{f\left( x \right)}}{{{x^3}}}}} = 1")
στην 
έχουμε:
οπότε 
είναι 
, οπότε :
διότι αποδείχθηκε πως λάθος δεν υπήρχε ). 
![\displaystyle{I = \int\limits_0^{\sqrt[3]{{10}}} {\left( {12x\int\limits_{\sqrt[3]{{10}}}^x {\frac{{f(t)}}{{3{f^2}(t) + 1}}dt} } \right)} dx = \int\limits_0^{\sqrt[3]{{10}}} {\left( {{{\left( {6{x^2}} \right)}^\prime }\int\limits_{\sqrt[3]{{10}}}^x {\frac{{f(t)}}{{3{f^2}(t) + 1}}dt} } \right)} dx}](/forum/ext/geomar/texintegr/latexrender/pictures/4f28b9207ac0250648019c5796422906.png "\displaystyle{I = \int\limits_0^{\sqrt[3]{{10}}} {\left( {12x\int\limits_{\sqrt[3]{{10}}}^x {\frac{{f(t)}}{{3{f^2}(t) + 1}}dt} } \right)} dx = \int\limits_0^{\sqrt[3]{{10}}} {\left( {{{\left( {6{x^2}} \right)}^\prime }\int\limits_{\sqrt[3]{{10}}}^x {\frac{{f(t)}}{{3{f^2}(t) + 1}}dt} } \right)} dx}")
![\displaystyle{{\left[ {6{x^2}\int\limits_{\sqrt[3]{{10}}}^x {\frac{{f(t)}}{{3{f^2}(x) + 1}}dt} } \right]^{\sqrt[3]{{10}}}}_0 - {\int\limits_0^{\sqrt[3]{{10}}} {6{x^2}\left( {\int\limits_{\sqrt[3]{{10}}}^x {\frac{{f(t)}}{{3{f^2}(x) + 1}}dt} } \right)} ^\prime }dt = }](/forum/ext/geomar/texintegr/latexrender/pictures/45fd6cd1f9483efdd3731f7abd667dec.png "\displaystyle{{\left[ {6{x^2}\int\limits_{\sqrt[3]{{10}}}^x {\frac{{f(t)}}{{3{f^2}(x) + 1}}dt} } \right]^{\sqrt[3]{{10}}}}_0 - {\int\limits_0^{\sqrt[3]{{10}}} {6{x^2}\left( {\int\limits_{\sqrt[3]{{10}}}^x {\frac{{f(t)}}{{3{f^2}(x) + 1}}dt} } \right)} ^\prime }dt = }")
![\displaystyle{0 - \int\limits_0^{\sqrt[3]{{10}}} {6{x^2}} \frac{{f(x)}}{{3{f^2}(x) + 1}}dx\mathop { = = = = = = = = = = }\limits^{f'(x) = \frac{{3{x^2}}}{{3{f^2}(x) + 1}}} \,\, - \int\limits_0^{\sqrt[3]{{10}}} {6{x^2}} \frac{{f(x)}}{{3{x^2}}}f'(x)dx = - \int\limits_0^{\sqrt[3]{{10}}} 2 f(x)f'(x)dx = }](/forum/ext/geomar/texintegr/latexrender/pictures/1267c2cae16d07f1e522762d2d6da564.png "\displaystyle{0 - \int\limits_0^{\sqrt[3]{{10}}} {6{x^2}} \frac{{f(x)}}{{3{f^2}(x) + 1}}dx\mathop { = = = = = = = = = = }\limits^{f'(x) = \frac{{3{x^2}}}{{3{f^2}(x) + 1}}} \,\, - \int\limits_0^{\sqrt[3]{{10}}} {6{x^2}} \frac{{f(x)}}{{3{x^2}}}f'(x)dx = - \int\limits_0^{\sqrt[3]{{10}}} 2 f(x)f'(x)dx = }")
![\displaystyle{ = - \left[ {{f^2}(x)} \right]_0^{\sqrt[3]{{10}}} = - \left( {{f^2}(\sqrt[3]{{10}}) - {f^2}(0)} \right) = - 4\,,\,}](/forum/ext/geomar/texintegr/latexrender/pictures/cc095001c313baf05602c2fe73628bb4.png "\displaystyle{ = - \left[ {{f^2}(x)} \right]_0^{\sqrt[3]{{10}}} = - \left( {{f^2}(\sqrt[3]{{10}}) - {f^2}(0)} \right) = - 4\,,\,}")
![\displaystyle{{f^{ - 1}}(2) = \sqrt[3]{{10}} \Rightarrow f\left( {\sqrt[3]{{10}}} \right) = 2.}](/forum/ext/geomar/texintegr/latexrender/pictures/642692fda949ee6fb500a9f18ae588cb.png "\displaystyle{{f^{ - 1}}(2) = \sqrt[3]{{10}} \Rightarrow f\left( {\sqrt[3]{{10}}} \right) = 2.}")
![\displaystyle f(x) = \sqrt[3]{{\sqrt {\frac{{{x^6}}}{4} + \frac{1}{{27}}} + \frac{{{x^3}}}{2}}} - \sqrt[3]{{\sqrt {\frac{{{x^6}}}{4} + \frac{1}{{27}}} - \frac{{{x^3}}}{2}}}](/forum/ext/geomar/texintegr/latexrender/pictures/e86758769eb3f88eddd6d8fa0a4d447e.png "\displaystyle f(x) = \sqrt[3]{{\sqrt {\frac{{{x^6}}}{4} + \frac{1}{{27}}} + \frac{{{x^3}}}{2}}} - \sqrt[3]{{\sqrt {\frac{{{x^6}}}{4} + \frac{1}{{27}}} - \frac{{{x^3}}}{2}}}")