 ώστε
ώστε 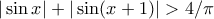 .
.Συντονιστής: Καρδαμίτσης Σπύρος
Γιαpeter έγραψε:Αποδείξτε ότι υπάρχειώστε
.
 στο πρώτο τεταρτημόριο οι παραστάσεις είναι θετικές, οπότε
στο πρώτο τεταρτημόριο οι παραστάσεις είναι θετικές, οπότε 

 ισούται
ισούται  .
. . Επομένως υπάρχει
. Επομένως υπάρχει  ώστε
ώστε  αφού αλλιώς θα είχαμε
αφού αλλιώς θα είχαμε 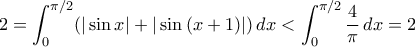 , όπου η αυστηρή ανισότητα έπεται επειδή η συνάρτηση
, όπου η αυστηρή ανισότητα έπεται επειδή η συνάρτηση  είναι συνεχής και δεν είναι ταυτοτικά ίση με
είναι συνεχής και δεν είναι ταυτοτικά ίση με  . Π.χ.
. Π.χ.  .
.Λίγο διαφορετικά από τον Μιχάλη.







![x\in [0,\pi -1] x\in [0,\pi -1]](/forum/ext/geomar/texintegr/latexrender/pictures/37cfdebf3f0307f749745a7c8114e9a1.png)
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες