Μια άσκηση με πολλά ερωτήματα, στηριγμένη σε άσκηση του σχολικού.
Μάλλον για θέμα Β. Ελπίζω να βοηθήσει τα παιδιά που δίνουν πανελλήνιες.
Εύχομαι ολόψυχα καλή επιτυχία !
Έστω η συνάρτηση
 .
.1. Να βρεθεί η εφαπτομένη της
 , η οποία διέρχεται από το σημείο
, η οποία διέρχεται από το σημείο  .
.2. Να μελετήσετε την
 ως προς την μονοτονία - ακρότατα και να βρείτε το σύνολο τιμών της
ως προς την μονοτονία - ακρότατα και να βρείτε το σύνολο τιμών της  .
.3. Να μελετήσετε την
 ως προς την κυρτότητα - σημεία καμπής και να βρείτε τις ασύμπτωτες της
ως προς την κυρτότητα - σημεία καμπής και να βρείτε τις ασύμπτωτες της  .
.4. Να βρεθεί το εμβαδόν του χωρίου που περικλείεται από την
 , την εφαπτομένη του 1ου ερωτήματος και την ευθεία
, την εφαπτομένη του 1ου ερωτήματος και την ευθεία  .
.5. Να βρεθεί το εμβαδόν
 του χωρίου, που περικλείεται από την
του χωρίου, που περικλείεται από την  , τον άξονα
, τον άξονα 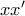 και την ευθεία
και την ευθεία  , με
, με  και
και  .
.Στη συνέχεια να υπολογίσετε το

Φιλικά
Σταμ. Γλάρος

 .
. οριστεί στο
οριστεί στο ![\displaystyle{(0,e]} \displaystyle{(0,e]}](/forum/ext/geomar/texintegr/latexrender/pictures/8c79d1fd7c0f3b1a303fb3fff0b769a6.png) , τότε αντιστρέφεται και να βρείτε το πεδίο ορισμού της αντίστροφης .
, τότε αντιστρέφεται και να βρείτε το πεδίο ορισμού της αντίστροφης . θεωρούμε τα σημεία
θεωρούμε τα σημεία  ,
,  των γραφικών παραστάσεων των συναρτήσεων
των γραφικών παραστάσεων των συναρτήσεων  , αντίστοιχα.
, αντίστοιχα. και
και  αντίστοιχα, είναι ίσο με
αντίστοιχα, είναι ίσο με 
 γίνεται ελάχιστη, και να βρείτε την ελάχιστη απόστασή τους.
γίνεται ελάχιστη, και να βρείτε την ελάχιστη απόστασή τους.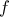 ορίζεται στο
ορίζεται στο 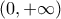 και είναι παραγωγίσιμη σ΄ αυτό με
και είναι παραγωγίσιμη σ΄ αυτό με 
 τυχαίο σημείο της
τυχαίο σημείο της 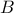 έχει εξίσωση :
έχει εξίσωση :

 έχει εξίσωση
έχει εξίσωση 
 . Επομένως η
. Επομένως η ![\displaystyle (0,e] \displaystyle (0,e]](/forum/ext/geomar/texintegr/latexrender/pictures/e6049b81bed7cd062339dc7a169b8309.png) και γνησίως φθίνουσα στο
και γνησίως φθίνουσα στο  .
. , ίσο με
, ίσο με 
 και
και 
![\displaystyle x\in (0,e] \displaystyle x\in (0,e]](/forum/ext/geomar/texintegr/latexrender/pictures/97203983de7e894540a57659399aec76.png) τότε
τότε ![\displaystyle f(x)\in \left( -\infty \right.,\left. \frac{1}{e} \right] \displaystyle f(x)\in \left( -\infty \right.,\left. \frac{1}{e} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/92b58bc7f89ee01bf28b668690f32315.png) και αν
και αν  τότε
τότε 
![\displaystyle \left( -\infty \right.,\left. \frac{1}{e} \right]\cup \left( \frac{1}{e},0 \right)=\left( -\infty \right.,\left. \frac{1}{e} \right] \displaystyle \left( -\infty \right.,\left. \frac{1}{e} \right]\cup \left( \frac{1}{e},0 \right)=\left( -\infty \right.,\left. \frac{1}{e} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/a0568aa58da3e8174cbf8690d3581f29.png)

 και
και  .
. και κυρτή αν
και κυρτή αν  . Άρα το
. Άρα το  είναι σημείο καμπής της
είναι σημείο καμπής της  .
. , η ευθεία
, η ευθεία  είναι κατακόρυφη ασύμπτωτη της
είναι κατακόρυφη ασύμπτωτη της  , η ευθεία
, η ευθεία  είναι οριζόντια ασύμπτωτη της
είναι οριζόντια ασύμπτωτη της ![\displaystyle x\in [1,e]\Rightarrow {f}''(x)\le 0 \displaystyle x\in [1,e]\Rightarrow {f}''(x)\le 0](/forum/ext/geomar/texintegr/latexrender/pictures/94479b03d05654937a9c488b96d0d13b.png) , οπότε η
, οπότε η ![\displaystyle \begin{array}{l}
E = \int_1^e {\left( {x - 1 - \frac{{\ln x}}{x}\,} \right)\,} dx = \int_1^e {(x - 1) - \,\,} \frac{1}{2}\int_1^e {2\ln x\frac{1}{x}\,\,} dx = \left[ {\frac{{{x^2}}}{2} - x} \right]_1^e - \frac{1}{2}\left[ {{{(\ln x)}^2}} \right]_1^e = \\
= \frac{{{e^2}}}{2} - e + \frac{1}{2} - \frac{1}{2}(1 - 0) = \frac{{{e^2}}}{2} - e
\end{array} \displaystyle \begin{array}{l}
E = \int_1^e {\left( {x - 1 - \frac{{\ln x}}{x}\,} \right)\,} dx = \int_1^e {(x - 1) - \,\,} \frac{1}{2}\int_1^e {2\ln x\frac{1}{x}\,\,} dx = \left[ {\frac{{{x^2}}}{2} - x} \right]_1^e - \frac{1}{2}\left[ {{{(\ln x)}^2}} \right]_1^e = \\
= \frac{{{e^2}}}{2} - e + \frac{1}{2} - \frac{1}{2}(1 - 0) = \frac{{{e^2}}}{2} - e
\end{array}](/forum/ext/geomar/texintegr/latexrender/pictures/2be407cf40f665c72177cbcf64db7e5f.png)
 τότε επειδή η
τότε επειδή η 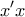 μόνο για
μόνο για  και
και  , θα είναι:
, θα είναι:![E(t)=\int_{1}^{t}{\frac{\ln x}{x}\,}dx=\frac{1}{2}\int_{1}^{t}{2\ln x\frac{1}{x}\,\,}dx=\frac{1}{2}\left[ {{(\ln x)}^{2}} \right]_{1}^{t}=\frac{1}{2}{{(\ln t)}^{2}} E(t)=\int_{1}^{t}{\frac{\ln x}{x}\,}dx=\frac{1}{2}\int_{1}^{t}{2\ln x\frac{1}{x}\,\,}dx=\frac{1}{2}\left[ {{(\ln x)}^{2}} \right]_{1}^{t}=\frac{1}{2}{{(\ln t)}^{2}}](/forum/ext/geomar/texintegr/latexrender/pictures/8c62c0156b09fe5f5f756b18f4a6f847.png)
 τότε επειδή η
τότε επειδή η  , θα είναι:
, θα είναι:![E(t)=-\int_{t}^{1}{\frac{\ln x}{x}\,}dx=\frac{1}{2}\int_{1}^{t}{2\ln x\frac{1}{x}\,\,}dx=\frac{1}{2}\left[ {{(\ln x)}^{2}} \right]_{1}^{t}=\frac{1}{2}{{(\ln t)}^{2}} E(t)=-\int_{t}^{1}{\frac{\ln x}{x}\,}dx=\frac{1}{2}\int_{1}^{t}{2\ln x\frac{1}{x}\,\,}dx=\frac{1}{2}\left[ {{(\ln x)}^{2}} \right]_{1}^{t}=\frac{1}{2}{{(\ln t)}^{2}}](/forum/ext/geomar/texintegr/latexrender/pictures/90eedaccc5577b7b7f58fd9df601b926.png) . Άρα
. Άρα ![\displaystyle \underset{t\to 0}{\mathop{\lim }}\,E(t)=\underset{t\to 0}{\mathop{\lim }}\,\left[ \frac{1}{2}{{(\ln t)}^{2}} \right]=+\infty \displaystyle \underset{t\to 0}{\mathop{\lim }}\,E(t)=\underset{t\to 0}{\mathop{\lim }}\,\left[ \frac{1}{2}{{(\ln t)}^{2}} \right]=+\infty](/forum/ext/geomar/texintegr/latexrender/pictures/92a608ebf3167791a24e067fe55178d6.png)
![(0,e] (0,e]](/forum/ext/geomar/texintegr/latexrender/pictures/1d8444b0b1caf41b600dce9babe7de1c.png) , άρα και 1-1.
, άρα και 1-1. .
. και
και  .
.![f\left ( (0,e] \right )=\left ( -\infty ,\dfrac{1}{e} \right ] f\left ( (0,e] \right )=\left ( -\infty ,\dfrac{1}{e} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/1e9365e579317318c825b2655ec7c429.png) , οπότε
, οπότε ![D_{f^{-1}}=\left ( -\infty ,\dfrac{1}{e} \right ] D_{f^{-1}}=\left ( -\infty ,\dfrac{1}{e} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/0da2df454b5441d2f28040b4b56f42c2.png) .
.

 με
με ![x\in\left ( -\infty ,\dfrac{1}{e} \right ] x\in\left ( -\infty ,\dfrac{1}{e} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/55e2b3bf6d273b6148fa15386f98cb8e.png) . Άρα
. Άρα  και
και  .
. .
. 

 .
. είναι η εφαπτομένη της
είναι η εφαπτομένη της  στο
στο  .
. . Άρα
. Άρα  .
. είναι η εφαπτομένη της
είναι η εφαπτομένη της  στο
στο  .
. εκτός από το σημείο επαφής.
εκτός από το σημείο επαφής. εκτός από το σημείο επαφής.
εκτός από το σημείο επαφής. είναι παράλληλες.
είναι παράλληλες. ,
,  είναι
είναι  .
.