erxmer έγραψε:Δίνεται η παραγωγίσιμη συνάρτηση

για την οποία ισχύουν:

1) Να αποδείξετε ότι ο τύπος της συνάρτησης

είναι

2) Να βρεθεί το σύνολο τιμών της συνάρτησης

3) Να δείξετε ότι η γραφική παράσταση της

έχει ακριβώς δυο σημεία καμπής

με
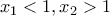
4) Δίνεται η συνάρτηση

. Να βρεθεί το εμβαδόν του χωρίου που περικλείεται από
τη γραφική παράσταση της συνάρτησης

, τον άξονα
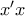
και τις ευθείες

και

.
...παρέα με τις ασκήσεις.....
1) Από

προκύπτει ότι

αφού από

έχουμε ότι

άρα

οπότε

Τώρα επειδή η

είναι παραγωγίσιμη στο

άρα και συνεχής θα ισχύει ότι

Είναι

και
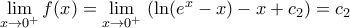
άρα

επομένως

και τελικά αφού
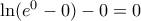
είναι

2) Είναι
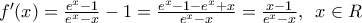
οπότε

και

άρα

γνήσια αύξουσα στο

και

άρα

γνήσια φθίνουσα στο
![{{\Delta }_{2}}=(-\infty ,1] {{\Delta }_{2}}=(-\infty ,1]](/forum/ext/geomar/texintegr/latexrender/pictures/d7618378b39b0f5df787e49a61c95822.png)
έτσι αφού η

είναι συνεχής έχουμε

Για το


αφού

και για το
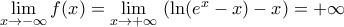
αφού

επομένως

άρα

3) Από
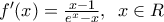
είναι

Τώρα η συνάρτηση

είναι συνεχής με

και

και

άρα

οπότε σύμφωνα με το Θεώρημα του Bolzano
υπάρχουν
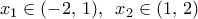
με

Τώρα επειδή

η συνάρτηση

είναι γνήσια αύξουσα στο διάστημα
![(-\infty ,\,\,1] (-\infty ,\,\,1]](/forum/ext/geomar/texintegr/latexrender/pictures/9a6e3d1e0498316cbabd3abc5d2e40af.png)
και γνήσια φθίνουσα στο διάστημα

επομένως
![{{x}_{1}}\in (-2,\,1)\subseteq (-\infty ,\,\,1] {{x}_{1}}\in (-2,\,1)\subseteq (-\infty ,\,\,1]](/forum/ext/geomar/texintegr/latexrender/pictures/35ee0997fb6de24c8ccaf6bb49fc0e2b.png)
είναι μοναδικό και

είναι μοναδικό και ακόμη
για

επομένως για την

ισχύει ότι

και αλλάζει πρόσημο εκατέρωθεν του
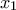
άρα το

μοναδικό σημείο καμπής στο
![(-\infty ,\,\,1] (-\infty ,\,\,1]](/forum/ext/geomar/texintegr/latexrender/pictures/9a6e3d1e0498316cbabd3abc5d2e40af.png)
και

επομένως για την

ισχύει ότι
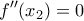
και αλλάζει πρόσημο εκατέρωθεν του

άρα
το

μοναδικό σημείο καμπής στο

άρα η

έχει ακριβώς δυο σημεία καμπής

με
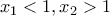
4) Το ζητούμενο εμβαδό θα είναι

και επειδή
![{{e}^{x}}\ge 1,\,\,\,x\in [0,\,\,1] {{e}^{x}}\ge 1,\,\,\,x\in [0,\,\,1]](/forum/ext/geomar/texintegr/latexrender/pictures/d30a66f1bed11e8adad6e679499a5445.png)
είναι

και ακόμη επειδή η

είναι γνήσια φθίνουσα στο
![(-\infty ,\,\,1] (-\infty ,\,\,1]](/forum/ext/geomar/texintegr/latexrender/pictures/9a6e3d1e0498316cbabd3abc5d2e40af.png)
με

για
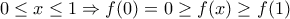
επομένως
![E=-\int\limits_{0}^{1}{({{e}^{x}}}-1)f(x)dx=-\int\limits_{0}^{1}{({{e}^{x}}}-x{)}'f(x)dx=-\left[ ({{e}^{x}}-x)f(x) \right]_{0}^{1}+\int\limits_{0}^{1}{({{e}^{x}}}-x){f}'(x)dx E=-\int\limits_{0}^{1}{({{e}^{x}}}-1)f(x)dx=-\int\limits_{0}^{1}{({{e}^{x}}}-x{)}'f(x)dx=-\left[ ({{e}^{x}}-x)f(x) \right]_{0}^{1}+\int\limits_{0}^{1}{({{e}^{x}}}-x){f}'(x)dx](/forum/ext/geomar/texintegr/latexrender/pictures/33fb0e5b104424288e7ab3ba60546ff9.png)
![\displaystyle{=-\left[ ({{e}^{x}}-x)f(x) \right]_{0}^{1}+\int\limits_{0}^{1}{({{e}^{x}}}-x)\frac{x-1}{{{e}^{x}}-x}dx=-\left[ ({{e}^{x}}-x)f(x) \right]_{0}^{1}+
\int\limits_{0}^{1}{(x-1)}dx=...} \displaystyle{=-\left[ ({{e}^{x}}-x)f(x) \right]_{0}^{1}+\int\limits_{0}^{1}{({{e}^{x}}}-x)\frac{x-1}{{{e}^{x}}-x}dx=-\left[ ({{e}^{x}}-x)f(x) \right]_{0}^{1}+
\int\limits_{0}^{1}{(x-1)}dx=...}](/forum/ext/geomar/texintegr/latexrender/pictures/0131b00884cb6b59f58d24317a8c5ab0.png)
Φιλικά και Μαθηματικά
Βασίλης
 για την οποία ισχύουν:
για την οποία ισχύουν: 
 είναι
είναι 

 έχει ακριβώς δυο σημεία καμπής
έχει ακριβώς δυο σημεία καμπής  με
με 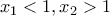
 . Να βρεθεί το εμβαδόν του χωρίου που περικλείεται από
. Να βρεθεί το εμβαδόν του χωρίου που περικλείεται από , τον άξονα
, τον άξονα 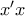 και τις ευθείες
και τις ευθείες  και
και  .
.
 προκύπτει ότι
προκύπτει ότι 
 έχουμε ότι
έχουμε ότι  άρα
άρα  οπότε
οπότε
 άρα και συνεχής θα ισχύει ότι
άρα και συνεχής θα ισχύει ότι 
 και
και 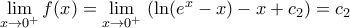
 επομένως
επομένως  και τελικά αφού
και τελικά αφού 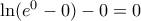 είναι
είναι 
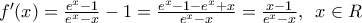 οπότε
οπότε  και
και  άρα
άρα  και
και 
![{{\Delta }_{2}}=(-\infty ,1] {{\Delta }_{2}}=(-\infty ,1]](/forum/ext/geomar/texintegr/latexrender/pictures/d7618378b39b0f5df787e49a61c95822.png) έτσι αφού η
έτσι αφού η 

 αφού
αφού 
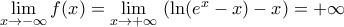
 επομένως
επομένως  άρα
άρα 
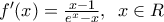 είναι
είναι 
 είναι συνεχής με
είναι συνεχής με  και
και  και
και  άρα
άρα  οπότε σύμφωνα με το Θεώρημα του Bolzano
οπότε σύμφωνα με το Θεώρημα του Bolzano 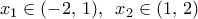 με
με 
 η συνάρτηση
η συνάρτηση ![(-\infty ,\,\,1] (-\infty ,\,\,1]](/forum/ext/geomar/texintegr/latexrender/pictures/9a6e3d1e0498316cbabd3abc5d2e40af.png)
 επομένως
επομένως ![{{x}_{1}}\in (-2,\,1)\subseteq (-\infty ,\,\,1] {{x}_{1}}\in (-2,\,1)\subseteq (-\infty ,\,\,1]](/forum/ext/geomar/texintegr/latexrender/pictures/35ee0997fb6de24c8ccaf6bb49fc0e2b.png)
 είναι μοναδικό και ακόμη
είναι μοναδικό και ακόμη 
 ισχύει ότι
ισχύει ότι  και αλλάζει πρόσημο εκατέρωθεν του
και αλλάζει πρόσημο εκατέρωθεν του 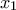
 μοναδικό σημείο καμπής στο
μοναδικό σημείο καμπής στο 
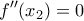 και αλλάζει πρόσημο εκατέρωθεν του
και αλλάζει πρόσημο εκατέρωθεν του  άρα
άρα  μοναδικό σημείο καμπής στο
μοναδικό σημείο καμπής στο  και επειδή
και επειδή ![{{e}^{x}}\ge 1,\,\,\,x\in [0,\,\,1] {{e}^{x}}\ge 1,\,\,\,x\in [0,\,\,1]](/forum/ext/geomar/texintegr/latexrender/pictures/d30a66f1bed11e8adad6e679499a5445.png) είναι
είναι  και ακόμη επειδή η
και ακόμη επειδή η  για
για 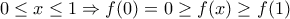 επομένως
επομένως ![E=-\int\limits_{0}^{1}{({{e}^{x}}}-1)f(x)dx=-\int\limits_{0}^{1}{({{e}^{x}}}-x{)}'f(x)dx=-\left[ ({{e}^{x}}-x)f(x) \right]_{0}^{1}+\int\limits_{0}^{1}{({{e}^{x}}}-x){f}'(x)dx E=-\int\limits_{0}^{1}{({{e}^{x}}}-1)f(x)dx=-\int\limits_{0}^{1}{({{e}^{x}}}-x{)}'f(x)dx=-\left[ ({{e}^{x}}-x)f(x) \right]_{0}^{1}+\int\limits_{0}^{1}{({{e}^{x}}}-x){f}'(x)dx](/forum/ext/geomar/texintegr/latexrender/pictures/33fb0e5b104424288e7ab3ba60546ff9.png)
![\displaystyle{=-\left[ ({{e}^{x}}-x)f(x) \right]_{0}^{1}+\int\limits_{0}^{1}{({{e}^{x}}}-x)\frac{x-1}{{{e}^{x}}-x}dx=-\left[ ({{e}^{x}}-x)f(x) \right]_{0}^{1}+
\int\limits_{0}^{1}{(x-1)}dx=...} \displaystyle{=-\left[ ({{e}^{x}}-x)f(x) \right]_{0}^{1}+\int\limits_{0}^{1}{({{e}^{x}}}-x)\frac{x-1}{{{e}^{x}}-x}dx=-\left[ ({{e}^{x}}-x)f(x) \right]_{0}^{1}+
\int\limits_{0}^{1}{(x-1)}dx=...}](/forum/ext/geomar/texintegr/latexrender/pictures/0131b00884cb6b59f58d24317a8c5ab0.png)