M.S.Vovos έγραψε:
Έστω η δύο φορές παραγωγίσιμη συνάρτηση

, για την οποία, για κάθε

, ισχύει:

 α)
α) Να αποδείξετε ότι η συνάρτηση

είναι γνησίως αύξουσα και κυρτή.
β) Να αποδείξετε ότι υπάρχει μοναδικό

τέτοιο, ώστε να ισχύει:
 γ)
γ) Να βρείτε το πεδίο ορισμού της συνάρτησης

.
δ) Αν

και

η μέγιστη και ελάχιστη τιμή της συνάρτησης

, αντίστοιχα, ώστε να ισχύει

, να αποδείξετε ότι υπάρχει

ώστε να ισχύει η ανισότητα:
![\displaystyle{\int_0^1 {{{\left[ {f\left( {\sqrt {x - {x^2}} } \right) - f'\left( x \right)} \right]}^2}} dx + \int_1^0 {f\left( {\sqrt {x - {x^2}} } \right)} \leqslant M - f'(t)- {{M}^2} } \displaystyle{\int_0^1 {{{\left[ {f\left( {\sqrt {x - {x^2}} } \right) - f'\left( x \right)} \right]}^2}} dx + \int_1^0 {f\left( {\sqrt {x - {x^2}} } \right)} \leqslant M - f'(t)- {{M}^2} }](/forum/ext/geomar/texintegr/latexrender/pictures/4956e986d25c4ced164403963cf04867.png) Φιλικά,
Φιλικά,
Μάριος
...άργα για νωρίς...
α) Επειδή από

προκύπτει ότι

,

και
αφού

συνεχής αφού είναι και παραγωγίσιμη θα έχει σταθερό πρόσημο στο

και επειδή

θα είναι

για κάθε

, οπότε η

είναι γνησίως αύξουσα .
Τώρα αν υπάρχουν

ώστε

τότε θα έχουμε

άρα

επομένως

οπότε το
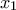
θέση τοπικού μεγίστου για την

και

επομένως

οπότε το

θέση τοπικού μεγίστου για την

και επομένως την ελάχιστη τιμή της η συνεχής

την παίρνει σε σημείο

και από Fermat

που είναι άτοπο.
Ανάλογα για τις άλλες περιπτώσεις μη σταθερού πρόσημου της

επομένως είναι

ή

Αν

τότε η

θα είναι γνήσια φθίνουσα στο

και θα ισχύει ότι

που είναι άτοπο άρα αναγκαία

που σημαίνει ότι η

είναι κυρτή στο

.
β) Για την συνάρτηση
![h(x)=2f(x+1)-f(x)-f(2)\,\,\,\,x\in [0,\,1] h(x)=2f(x+1)-f(x)-f(2)\,\,\,\,x\in [0,\,1]](/forum/ext/geomar/texintegr/latexrender/pictures/debb33bb58e0aebc8c790a7009b99008.png)
είναι συνεχής
ως πράξεις συνεχών με

και

αφού η

είναι γνήσια αύξουσα .
Τώρα

και σύμφωνα με το Θ.Μ.Τ στα
![[0,\,1],\,\,[1,\,2] [0,\,1],\,\,[1,\,2]](/forum/ext/geomar/texintegr/latexrender/pictures/a79d4598ae00a02a0295f83c62dc469a.png)
υπάρχουν

που

έτσι

επειδή η

είναι γνήσια αύξουσα και

έτσι

και σύμφωνα με το θεώρημα του Bolzano η

έχει ρίζα στο
 Τώρα για την μοναδικότητα
Τώρα για την μοναδικότητα Αν υποθέσουμε ότι η εξίσωση έχει δύο ρίζες στο

τις

τότε είναι

και επειδή η

είναι παραγωγίσιμη με

σύμφωνα με το θεώρημα του Rolle υπάρχει

ώστε

που είναι άτοπο γιατί

και

αφού

άρα ισχύει

γ) Η συνάρτηση

ορίζεται όταν και μόνο όταν
 ...και μετά την διόρθωση του δημιουργού....
...και μετά την διόρθωση του δημιουργού....
δ) Θέλουμε να δείξουμε ότι υπάρχει

ώστε
![\int\limits_{0}^{1}{{{\left[ f\left( \sqrt{x-{{x}^{2}}} \right)-{f}'\left( x \right) \right]}^{2}}}dx+\int\limits_{1}^{0}{f\left( \sqrt{x-{{x}^{2}}} \right)}M-{f}'(t)-{{M}^{2}}\Leftrightarrow \int\limits_{0}^{1}{{{\left[ f\left( \sqrt{x-{{x}^{2}}} \right)-{f}'\left( x \right) \right]}^{2}}}dx+\int\limits_{1}^{0}{f\left( \sqrt{x-{{x}^{2}}} \right)}M-{f}'(t)-{{M}^{2}}\Leftrightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/f12c797e055849d8fc1e8e776273453d.png)
![\int\limits_{0}^{1}{{{\left[ g(x) \right]}^{2}}}dx+\int\limits_{1}^{0}{\left( g(x)+{f}'(x) \right)dx}M-{f}'(t)-{{M}^{2}}\Leftrightarrow \int\limits_{0}^{1}{{{\left[ g(x) \right]}^{2}}}dx+\int\limits_{1}^{0}{\left( g(x)+{f}'(x) \right)dx}M-{f}'(t)-{{M}^{2}}\Leftrightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/79b39103e825883e8b3d031c74258d1f.png)
![\int\limits_{0}^{1}{{{\left[ g(x) \right]}^{2}}}dx-\int\limits_{0}^{1}{\left( g(x)+{f}'(x) \right)dx}M-{f}'(t)-{{M}^{2}}\Leftrightarrow \int\limits_{0}^{1}{{{\left[ g(x) \right]}^{2}}}dx-\int\limits_{0}^{1}{\left( g(x)+{f}'(x) \right)dx}M-{f}'(t)-{{M}^{2}}\Leftrightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/324180fe5327d0d2c905ae5376bc400b.png)
![\int\limits_{0}^{1}{{{\left[ g(x) \right]}^{2}}}dx-\int\limits_{0}^{1}{\left( g(x) \right)dx-}\int\limits_{0}^{1}{\left( {f}'(x) \right)dx}M-{f}'(t)-{{M}^{2}}\Leftrightarrow \int\limits_{0}^{1}{{{\left[ g(x) \right]}^{2}}}dx-\int\limits_{0}^{1}{\left( g(x) \right)dx-}\int\limits_{0}^{1}{\left( {f}'(x) \right)dx}M-{f}'(t)-{{M}^{2}}\Leftrightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/ca5736da94b6030cc8498decdcda22b6.png)
![\int\limits_{0}^{1}{{{\left[ g(x) \right]}^{2}}}dx-\int\limits_{0}^{1}{\left( g(x) \right)dx+{{M}^{2}}-M-}(f(1)-f(0))\le -{f}'(t) \int\limits_{0}^{1}{{{\left[ g(x) \right]}^{2}}}dx-\int\limits_{0}^{1}{\left( g(x) \right)dx+{{M}^{2}}-M-}(f(1)-f(0))\le -{f}'(t)](/forum/ext/geomar/texintegr/latexrender/pictures/56a5f4b9a4ff1bbf59a56c6154150813.png)
(1)
Είναι

άρα

επομένως

και ολοκληρώνοντας έχουμε
![\int\limits_{0}^{1}{{{\left[ g(x) \right]}^{2}}}dx-\int\limits_{0}^{1}{\left( g(x) \right)dx+{{M}^{2}}-M\le 0} \int\limits_{0}^{1}{{{\left[ g(x) \right]}^{2}}}dx-\int\limits_{0}^{1}{\left( g(x) \right)dx+{{M}^{2}}-M\le 0}](/forum/ext/geomar/texintegr/latexrender/pictures/ce9b9ae6a4f0802a1fb37d3755dde602.png)
Τώρα από Θ.Μ.Τ. υπάρχει

ώστε

άρα υπάρχει

ώστε να ισχύει ότι
![\displaystyle{\int\limits_{0}^{1}{{{\left[ g(x) \right]}^{2}}}dx-\int\limits_{0}^{1}{\left( g(x) \right)dx+{{M}^{2}}-M\le }f(1)-f(0)-{f}'(t)} \displaystyle{\int\limits_{0}^{1}{{{\left[ g(x) \right]}^{2}}}dx-\int\limits_{0}^{1}{\left( g(x) \right)dx+{{M}^{2}}-M\le }f(1)-f(0)-{f}'(t)}](/forum/ext/geomar/texintegr/latexrender/pictures/e9e580a522c0793210ad9f1b4fc84589.png)
...Συμπλήρωσα την μοναδικότητα στο(β) και την απάντηση στο(δ)
Φιλικά και Μαθηματικά
Βασίλης
 , για την οποία, για κάθε
, για την οποία, για κάθε  , ισχύει:
, ισχύει:
 α) Να αποδείξετε ότι η συνάρτηση
α) Να αποδείξετε ότι η συνάρτηση  είναι γνησίως αύξουσα και κυρτή.
είναι γνησίως αύξουσα και κυρτή. τέτοιο, ώστε να ισχύει:
τέτοιο, ώστε να ισχύει: 
 .
. και
και  η μέγιστη και ελάχιστη τιμή της συνάρτησης
η μέγιστη και ελάχιστη τιμή της συνάρτησης  , αντίστοιχα, ώστε να ισχύει
, αντίστοιχα, ώστε να ισχύει  , να αποδείξετε ότι υπάρχει
, να αποδείξετε ότι υπάρχει  ώστε να ισχύει η ανισότητα:
ώστε να ισχύει η ανισότητα:![\displaystyle{\int_0^1 {{{\left[ {f\left( {\sqrt {x - {x^2}} } \right) - f'\left( x \right)} \right]}^2}} dx + \int_1^0 {f\left( {\sqrt {x - {x^2}} } \right)} \leqslant {{M}^2} }- f'(t)+M \displaystyle{\int_0^1 {{{\left[ {f\left( {\sqrt {x - {x^2}} } \right) - f'\left( x \right)} \right]}^2}} dx + \int_1^0 {f\left( {\sqrt {x - {x^2}} } \right)} \leqslant {{M}^2} }- f'(t)+M](/forum/ext/geomar/texintegr/latexrender/pictures/56e96353e13433e1e223f3187033306f.png) Φιλικά,
Φιλικά,
![\displaystyle{\int_0^1 {{{\left[ {f\left( {\sqrt {x - {x^2}} } \right) - f'\left( x \right)} \right]}^2}} dx + \int_1^0 {f\left( {\sqrt {x - {x^2}} } \right)} \leqslant M - f'(t)- {{M}^2} } \displaystyle{\int_0^1 {{{\left[ {f\left( {\sqrt {x - {x^2}} } \right) - f'\left( x \right)} \right]}^2}} dx + \int_1^0 {f\left( {\sqrt {x - {x^2}} } \right)} \leqslant M - f'(t)- {{M}^2} }](/forum/ext/geomar/texintegr/latexrender/pictures/4956e986d25c4ced164403963cf04867.png)
 ,
,  και
και  συνεχής αφού είναι και παραγωγίσιμη θα έχει σταθερό πρόσημο στο
συνεχής αφού είναι και παραγωγίσιμη θα έχει σταθερό πρόσημο στο  και επειδή
και επειδή  θα είναι
θα είναι  για κάθε
για κάθε  ώστε
ώστε  τότε θα έχουμε
τότε θα έχουμε  άρα
άρα  επομένως
επομένως 
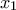 θέση τοπικού μεγίστου για την
θέση τοπικού μεγίστου για την  επομένως
επομένως 
 θέση τοπικού μεγίστου για την
θέση τοπικού μεγίστου για την  και από Fermat
και από Fermat  που είναι άτοπο.
που είναι άτοπο. επομένως είναι
επομένως είναι  ή
ή 
 και θα ισχύει ότι
και θα ισχύει ότι 
![h(x)=2f(x+1)-f(x)-f(2)\,\,\,\,x\in [0,\,1] h(x)=2f(x+1)-f(x)-f(2)\,\,\,\,x\in [0,\,1]](/forum/ext/geomar/texintegr/latexrender/pictures/debb33bb58e0aebc8c790a7009b99008.png) είναι συνεχής
είναι συνεχής  και
και  αφού η
αφού η  και σύμφωνα με το Θ.Μ.Τ στα
και σύμφωνα με το Θ.Μ.Τ στα ![[0,\,1],\,\,[1,\,2] [0,\,1],\,\,[1,\,2]](/forum/ext/geomar/texintegr/latexrender/pictures/a79d4598ae00a02a0295f83c62dc469a.png) υπάρχουν
υπάρχουν 
 έτσι
έτσι  επειδή η
επειδή η 
 έχει ρίζα στο
έχει ρίζα στο 
 τις
τις  τότε είναι
τότε είναι  και επειδή η
και επειδή η  είναι παραγωγίσιμη με
είναι παραγωγίσιμη με 
 ώστε
ώστε 

 αφού
αφού 

![\int\limits_{0}^{1}{{{\left[ f\left( \sqrt{x-{{x}^{2}}} \right)-{f}'\left( x \right) \right]}^{2}}}dx+\int\limits_{1}^{0}{f\left( \sqrt{x-{{x}^{2}}} \right)}M-{f}'(t)-{{M}^{2}}\Leftrightarrow \int\limits_{0}^{1}{{{\left[ f\left( \sqrt{x-{{x}^{2}}} \right)-{f}'\left( x \right) \right]}^{2}}}dx+\int\limits_{1}^{0}{f\left( \sqrt{x-{{x}^{2}}} \right)}M-{f}'(t)-{{M}^{2}}\Leftrightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/f12c797e055849d8fc1e8e776273453d.png)
![\int\limits_{0}^{1}{{{\left[ g(x) \right]}^{2}}}dx+\int\limits_{1}^{0}{\left( g(x)+{f}'(x) \right)dx}M-{f}'(t)-{{M}^{2}}\Leftrightarrow \int\limits_{0}^{1}{{{\left[ g(x) \right]}^{2}}}dx+\int\limits_{1}^{0}{\left( g(x)+{f}'(x) \right)dx}M-{f}'(t)-{{M}^{2}}\Leftrightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/79b39103e825883e8b3d031c74258d1f.png)
![\int\limits_{0}^{1}{{{\left[ g(x) \right]}^{2}}}dx-\int\limits_{0}^{1}{\left( g(x)+{f}'(x) \right)dx}M-{f}'(t)-{{M}^{2}}\Leftrightarrow \int\limits_{0}^{1}{{{\left[ g(x) \right]}^{2}}}dx-\int\limits_{0}^{1}{\left( g(x)+{f}'(x) \right)dx}M-{f}'(t)-{{M}^{2}}\Leftrightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/324180fe5327d0d2c905ae5376bc400b.png)
![\int\limits_{0}^{1}{{{\left[ g(x) \right]}^{2}}}dx-\int\limits_{0}^{1}{\left( g(x) \right)dx-}\int\limits_{0}^{1}{\left( {f}'(x) \right)dx}M-{f}'(t)-{{M}^{2}}\Leftrightarrow \int\limits_{0}^{1}{{{\left[ g(x) \right]}^{2}}}dx-\int\limits_{0}^{1}{\left( g(x) \right)dx-}\int\limits_{0}^{1}{\left( {f}'(x) \right)dx}M-{f}'(t)-{{M}^{2}}\Leftrightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/ca5736da94b6030cc8498decdcda22b6.png)
![\int\limits_{0}^{1}{{{\left[ g(x) \right]}^{2}}}dx-\int\limits_{0}^{1}{\left( g(x) \right)dx+{{M}^{2}}-M-}(f(1)-f(0))\le -{f}'(t) \int\limits_{0}^{1}{{{\left[ g(x) \right]}^{2}}}dx-\int\limits_{0}^{1}{\left( g(x) \right)dx+{{M}^{2}}-M-}(f(1)-f(0))\le -{f}'(t)](/forum/ext/geomar/texintegr/latexrender/pictures/56a5f4b9a4ff1bbf59a56c6154150813.png) (1)
(1) άρα
άρα  επομένως
επομένως  και ολοκληρώνοντας έχουμε
και ολοκληρώνοντας έχουμε ![\int\limits_{0}^{1}{{{\left[ g(x) \right]}^{2}}}dx-\int\limits_{0}^{1}{\left( g(x) \right)dx+{{M}^{2}}-M\le 0} \int\limits_{0}^{1}{{{\left[ g(x) \right]}^{2}}}dx-\int\limits_{0}^{1}{\left( g(x) \right)dx+{{M}^{2}}-M\le 0}](/forum/ext/geomar/texintegr/latexrender/pictures/ce9b9ae6a4f0802a1fb37d3755dde602.png)
 ώστε
ώστε 
![\displaystyle{\int\limits_{0}^{1}{{{\left[ g(x) \right]}^{2}}}dx-\int\limits_{0}^{1}{\left( g(x) \right)dx+{{M}^{2}}-M\le }f(1)-f(0)-{f}'(t)} \displaystyle{\int\limits_{0}^{1}{{{\left[ g(x) \right]}^{2}}}dx-\int\limits_{0}^{1}{\left( g(x) \right)dx+{{M}^{2}}-M\le }f(1)-f(0)-{f}'(t)}](/forum/ext/geomar/texintegr/latexrender/pictures/e9e580a522c0793210ad9f1b4fc84589.png)