 για την οποία ισχύει :
για την οποία ισχύει :  , για κάθε
, για κάθε  .
.Β1. Να δείξετε ότι

Β2. Να μελετήσετε την
 ως προς τη μονοτονία , την κυρτότητα , τις ασύμπτωτες και να βρείτε το σύνολο τιμών της .
ως προς τη μονοτονία , την κυρτότητα , τις ασύμπτωτες και να βρείτε το σύνολο τιμών της .Β3. Να δείξετε ότι
 για κάθε ,
για κάθε , με
με  .
.Β4. Να υπολογίσετε το
 και το
και το 
Συντονιστής: Καρδαμίτσης Σπύρος
 για την οποία ισχύει :
για την οποία ισχύει :  , για κάθε
, για κάθε  .
.
 ως προς τη μονοτονία , την κυρτότητα , τις ασύμπτωτες και να βρείτε το σύνολο τιμών της .
ως προς τη μονοτονία , την κυρτότητα , τις ασύμπτωτες και να βρείτε το σύνολο τιμών της . για κάθε ,
για κάθε , με
με  .
. και το
και το 
...και μιά απλή αντιμετώπιση...exdx έγραψε:Έστω η συνάρτησηγια την οποία ισχύει :
, για κάθε
.
Β1. Να δείξετε ότι
Β2. Να μελετήσετε τηνως προς τη μονοτονία , την κυρτότητα , τις ασύμπτωτες και να βρείτε το σύνολο τιμών της .
Β3. Να δείξετε ότιγια κάθε ,
με
.
Β4. Να υπολογίσετε τοκαι το


 είναι παραγωγίσιμη ως πράξεις παραγωγίσιμων και από
είναι παραγωγίσιμη ως πράξεις παραγωγίσιμων και από  παραγωγίζοντας έχουμε ότι
παραγωγίζοντας έχουμε ότι  άρα η συνάρτηση
άρα η συνάρτηση  είναι γνήσια αύξουσα στο
είναι γνήσια αύξουσα στο
 επομένως είναι και κοίλη στο
επομένως είναι και κοίλη στο  .
. το
το 
 δηλαδή ο
δηλαδή ο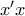 είναι ασύμπτωτη της γραφικής παράστασης της
είναι ασύμπτωτη της γραφικής παράστασης της  στο
στο  και επειδή
και επειδή  το
το 

 είναι συνεχής στο
είναι συνεχής στο  δεν έχει κατακόρυφες ασύμπτωτες και στο
δεν έχει κατακόρυφες ασύμπτωτες και στο  είναι
είναι  και
και 
 είναι ασύμπτωτη της της γραφικής παράστασης της
είναι ασύμπτωτη της της γραφικής παράστασης της  στο
στο 
 (1)
(1) στο διάστημα που ορίζουν τα
στο διάστημα που ορίζουν τα  με
με  που
που  και από (1)
και από (1) που ισχύει.
που ισχύει. και από
και από  άρα
άρα ![{{\Iota }_{1}}=\int\limits_{0}^{1}{\left( 1-\frac{{{e}^{x}}}{{{e}^{x}}+1} \right)dx}=\left[ x-\ln ({{e}^{x}}+1) \right]_{0}^{1}=1-\ln (e+1)+ln2 {{\Iota }_{1}}=\int\limits_{0}^{1}{\left( 1-\frac{{{e}^{x}}}{{{e}^{x}}+1} \right)dx}=\left[ x-\ln ({{e}^{x}}+1) \right]_{0}^{1}=1-\ln (e+1)+ln2](/forum/ext/geomar/texintegr/latexrender/pictures/30063ed77d6b11b3405230fe83967c0d.png)
![{{I}_{2}}=\int\limits_{0}^{1}{{{e}^{x}}\ln \left( \frac{{{e}^{x}}}{{{e}^{x}}+1} \right)dx}=\int\limits_{0}^{1}{{{e}^{x}}f(x)dx}=\left[ {{e}^{x}}f(x) \right]_{0}^{1}-\int\limits_{0}^{1}{{{e}^{x}}{f}'(x)dx}= {{I}_{2}}=\int\limits_{0}^{1}{{{e}^{x}}\ln \left( \frac{{{e}^{x}}}{{{e}^{x}}+1} \right)dx}=\int\limits_{0}^{1}{{{e}^{x}}f(x)dx}=\left[ {{e}^{x}}f(x) \right]_{0}^{1}-\int\limits_{0}^{1}{{{e}^{x}}{f}'(x)dx}=](/forum/ext/geomar/texintegr/latexrender/pictures/a08486aace704d8c18f20d3695064466.png)
![\left[ ef(1)-f(0) \right]-\int\limits_{0}^{1}{\frac{{{e}^{x}}}{{{e}^{x}}+1}dx}=ef(1)-f(0)-\left[ \ln ({{e}^{x}}+1) \right]_{0}^{1}=.... \left[ ef(1)-f(0) \right]-\int\limits_{0}^{1}{\frac{{{e}^{x}}}{{{e}^{x}}+1}dx}=ef(1)-f(0)-\left[ \ln ({{e}^{x}}+1) \right]_{0}^{1}=....](/forum/ext/geomar/texintegr/latexrender/pictures/6548471f278c88bb1a727403d15f31fd.png)

 όπως έδειξε ο Βασίλης είναι γνησίως αύξουσα.
όπως έδειξε ο Βασίλης είναι γνησίως αύξουσα. είναι
είναι 



Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες