erxmer έγραψε:Δίνονται οι συναρτήσεις

με

.
1) Να αποδείξετε ότι οι συναρτήσεις δέχονται δυο κοινές εφαπτομένες.
2) Να υπολογίσετε το όριο

3) Να βρείτε την αντίστροφη συνάρτηση της

στα διαστήματα όπου αυτή ορίζεται και στη συνέχεια να υπολογίσετε το εμβαδόν που περικλείεται από τις γραφικές παραστάσεις των συναρτήσεων

και

.
4) Να αποδείξετε ότι η συνάρτηση

, έχει ένα τουλάχιστον ακρότατο

, με

5) Αν

, νδο

Καλησπέρα. Μια προσπάθεια στα δύο πρώτα...
1) Η εξίσωση της εφαπτομένης της

στο σημείο

είναι :

Επίσης η εξίσωση της εφαπτομένης της

στο σημείο

είναι :

Για να είναι κοινή εφαπτομένη πρέπει να ισχύουν:

(1) και

(2).
Αντικαθιστώντας στην (2) την (1) προκύπτει:

Θεωρώντας, τώρα, την

έχουμε :

Από τα παραπάνω προκύπτει:
Για

. Συνεπώς η

είναι γνησίως φθίνουσα στο
![(0, \frac{\sqrt{2}}{2}] (0, \frac{\sqrt{2}}{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/ab4a0cd974c5a5387779f1992bd67b6d.png)
.
Για

. Συνεπώς η

είναι γνησίως αύξουσα στο

.
Επίσης έχουμε:

,

και

.
Ισχύουν οι προϋποθέσεις του Θεωρήματος Bolzano για την

στο
![\left [ \dfrac{1}{e^2} , \dfrac{\sqrt{2}}{2}\right ] \left [ \dfrac{1}{e^2} , \dfrac{\sqrt{2}}{2}\right ]](/forum/ext/geomar/texintegr/latexrender/pictures/0f90654e78e770389ef5a3c51067c059.png)
.
Άρα υπάρχει τουλάχιστον μία ρίζα της

στο

, η οποία λόγω μονοτονίας είναι μοναδική στο
![\left ( 0 , \dfrac{\sqrt{2}}{2}\right ] \left ( 0 , \dfrac{\sqrt{2}}{2}\right ]](/forum/ext/geomar/texintegr/latexrender/pictures/7298f23f166da627d0393a8c21793f7c.png)
.
Επίσης ισχύουν οι προϋποθέσεις του Θεωρήματος Bolzano για την

στο
![\left [ \dfrac{\sqrt{2}}{2} , e\right ] \left [ \dfrac{\sqrt{2}}{2} , e\right ]](/forum/ext/geomar/texintegr/latexrender/pictures/a2cc8a1a95c9f932dd986b810ccb810b.png)
.
Άρα υπάρχει τουλάχιστον μία ρίζα της

στο

, η οποία λόγω μονοτονίας είναι μοναδική στο

.
Από τα παραπάνω προκύπτει ότι οι συναρτήσεις δέχονται δυο κοινές εφαπτομένες.
2) Κατά τα γνωστά είναι

Επομένως


.
Το παραπάνω ισχύει διότι :
α) Θέτοντας

είναι :

, οπότε

και εφαρμόζοντας κανόνα de L' Hospital ( μορφή:

έχουμε:
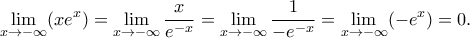
Φιλικά
Σταμ. Γλάρος
 με
με  .
.
 στα διαστήματα όπου αυτή ορίζεται και στη συνέχεια να υπολογίσετε το εμβαδόν που περικλείεται από τις γραφικές παραστάσεις των συναρτήσεων
στα διαστήματα όπου αυτή ορίζεται και στη συνέχεια να υπολογίσετε το εμβαδόν που περικλείεται από τις γραφικές παραστάσεις των συναρτήσεων  και
και  .
. , έχει ένα τουλάχιστον ακρότατο
, έχει ένα τουλάχιστον ακρότατο  , με
, με
 , νδο
, νδο 

 στο σημείο
στο σημείο  είναι :
είναι : 
 στο σημείο
στο σημείο  είναι :
είναι : 
 (1) και
(1) και  (2).
(2).
 έχουμε :
έχουμε : 
 . Συνεπώς η
. Συνεπώς η  είναι γνησίως φθίνουσα στο
είναι γνησίως φθίνουσα στο ![(0, \frac{\sqrt{2}}{2}] (0, \frac{\sqrt{2}}{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/ab4a0cd974c5a5387779f1992bd67b6d.png) .
. . Συνεπώς η
. Συνεπώς η  .
. ,
,  και
και  .
. ![\left [ \dfrac{1}{e^2} , \dfrac{\sqrt{2}}{2}\right ] \left [ \dfrac{1}{e^2} , \dfrac{\sqrt{2}}{2}\right ]](/forum/ext/geomar/texintegr/latexrender/pictures/0f90654e78e770389ef5a3c51067c059.png) .
. , η οποία λόγω μονοτονίας είναι μοναδική στο
, η οποία λόγω μονοτονίας είναι μοναδική στο ![\left ( 0 , \dfrac{\sqrt{2}}{2}\right ] \left ( 0 , \dfrac{\sqrt{2}}{2}\right ]](/forum/ext/geomar/texintegr/latexrender/pictures/7298f23f166da627d0393a8c21793f7c.png) .
.![\left [ \dfrac{\sqrt{2}}{2} , e\right ] \left [ \dfrac{\sqrt{2}}{2} , e\right ]](/forum/ext/geomar/texintegr/latexrender/pictures/a2cc8a1a95c9f932dd986b810ccb810b.png) .
. , η οποία λόγω μονοτονίας είναι μοναδική στο
, η οποία λόγω μονοτονίας είναι μοναδική στο  .
.

 .
. είναι :
είναι :  , οπότε
, οπότε 
 έχουμε:
έχουμε: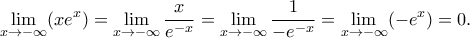
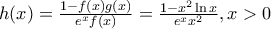 παραγωγίσιμη με
παραγωγίσιμη με 
 που είναι συνεχής με
που είναι συνεχής με  και
και  αφου το
αφου το  σύμφωνα με το Θ. Bolzano έχει τουλάχιστον μία ρίζα
σύμφωνα με το Θ. Bolzano έχει τουλάχιστον μία ρίζα  η
η  είναι γνήσια αύξουσα στο
είναι γνήσια αύξουσα στο  άρα και
άρα και  επομένως η ρίζα
επομένως η ρίζα  και για
και για 
 έχουμε αντίστοιχα ότι
έχουμε αντίστοιχα ότι 
 και ότι για
και ότι για 
![(0,\,\,{{x}_{0}}] (0,\,\,{{x}_{0}}]](/forum/ext/geomar/texintegr/latexrender/pictures/5342201b795a013f349d4a31d0247a61.png) επομένως παρουσιάζει ολικό ακρότατο στο
επομένως παρουσιάζει ολικό ακρότατο στο  και επειδή
και επειδή 
 θα είναι
θα είναι 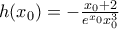


![={{I}_{n-1}}+\frac{1}{2n}\int\limits_{-1}^{1}{{{\left( {{\left( 1-{{x}^{2}} \right)}^{n}} \right)}^{\prime }}x}dx={{I}_{n-1}}+\left[ {{\left( 1-{{x}^{2}} \right)}^{n}}x \right]_{0}^{1}-\frac{1}{2n}{{I}_{n}} ={{I}_{n-1}}+\frac{1}{2n}\int\limits_{-1}^{1}{{{\left( {{\left( 1-{{x}^{2}} \right)}^{n}} \right)}^{\prime }}x}dx={{I}_{n-1}}+\left[ {{\left( 1-{{x}^{2}} \right)}^{n}}x \right]_{0}^{1}-\frac{1}{2n}{{I}_{n}}](/forum/ext/geomar/texintegr/latexrender/pictures/9c90bd3ef6fc9f6fc40a49c4d2ab199d.png)

![\displaystyle{E = \int\limits_0^1 {(\sqrt x - {x^2})} dx = \left[ {\frac{2}{3}{x^{\frac{3}{2}}} - \frac{{{x^3}}}{3}} \right]_0^1 = \frac{1}{3}} \displaystyle{E = \int\limits_0^1 {(\sqrt x - {x^2})} dx = \left[ {\frac{2}{3}{x^{\frac{3}{2}}} - \frac{{{x^3}}}{3}} \right]_0^1 = \frac{1}{3}}](/forum/ext/geomar/texintegr/latexrender/pictures/2c89574f8eb944e2f1f281e7021de2e0.png)