 συμβολίζουμε το ημίτονο και με
συμβολίζουμε το ημίτονο και με 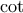 τη συνεφαπτομένη. Έστω η παραγωγίσιμη συνάρτηση
τη συνεφαπτομένη. Έστω η παραγωγίσιμη συνάρτηση 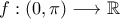 , με
, με  τέτοια, ώστε για κάθε
τέτοια, ώστε για κάθε  να ισχύει:
να ισχύει:
- Να αποδείξετε ότι η συνάρτηση
 είναι σταθερή στο
είναι σταθερή στο  και να προσδιορίσετε τον τύπο της
και να προσδιορίσετε τον τύπο της  .
.
Για τα ερωτήματα (β') και (γ'), δίνεται ότι
 ,
,  .
.- Να αποδείξετε ότι η γραφική παράσταση της
 τέμνει την διχοτόμο του πρώτου και τρίτου τεταρτημορίου σε ακριβώς δύο σημεία, έστω
τέμνει την διχοτόμο του πρώτου και τρίτου τεταρτημορίου σε ακριβώς δύο σημεία, έστω  και
και  με
με  και
και  .
.
- Να αποδείξετε ότι η
 είναι κυρτή στο
είναι κυρτή στο  . Στη συνέχεια, ορίζουμε ως μέση τιμή
. Στη συνέχεια, ορίζουμε ως μέση τιμή  το ημιάθροισμα των τετμημένων των σημείων
το ημιάθροισμα των τετμημένων των σημείων  και
και  του ερωτήματος (β'). Να συγκρίνετε τους αριθμούς
του ερωτήματος (β'). Να συγκρίνετε τους αριθμούς  και
και 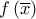 .
.
Μάριος

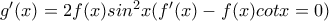 από την δοθείσα. (Ισχύει ότι:
από την δοθείσα. (Ισχύει ότι:  )
) και επειδή
και επειδή  , συμπεραίνουμε
, συμπεραίνουμε  .
. ,
,  .
.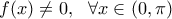 και επειδή η
και επειδή η  . Άρα
. Άρα  και
και  .
.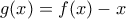 . Είναι
. Είναι  , διότι
, διότι  ,
,  όταν
όταν  άρα
άρα  .
. κοντά στο
κοντά στο  ώστε
ώστε  .
. .
.![[a,\frac{\pi}{2}] [a,\frac{\pi}{2}]](/forum/ext/geomar/texintegr/latexrender/pictures/b9f8ea6b9cf21c10249cbbf9681279f2.png) .
. ώστε
ώστε  δηλαδή
δηλαδή  .
.![[\frac{\pi}{2} , \pi] [\frac{\pi}{2} , \pi]](/forum/ext/geomar/texintegr/latexrender/pictures/c98c8e5c4163b32e37273ea63c62a218.png) προκύπτει
προκύπτει  δηλαδή
δηλαδή  .
. και
και  .
. γνησίως αύξουσα.
γνησίως αύξουσα. έχει τρεις ρίζες στο
έχει τρεις ρίζες στο  , άτοπο αφού η
, άτοπο αφού η ![[x_1,\overline{x}] [x_1,\overline{x}]](/forum/ext/geomar/texintegr/latexrender/pictures/5554862ecbf83dc0f078d588038f0acf.png) έχουμε ότι υπάρχει τουλάχιστον ένα
έχουμε ότι υπάρχει τουλάχιστον ένα  ώστε
ώστε 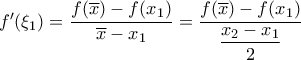 .
.![[\overline{x} , x_2] [\overline{x} , x_2]](/forum/ext/geomar/texintegr/latexrender/pictures/31fa11a5bf59cbf8a559364902f3f728.png) έχουμε ότι υπάρχει τουλάχιστον ένα
έχουμε ότι υπάρχει τουλάχιστον ένα  ώστε
ώστε  .
. είναι γνησίως αύξουσα αφού η
είναι γνησίως αύξουσα αφού η 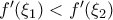 , οπότε προκύπτει
, οπότε προκύπτει  , από το προηγούμενο υποερώτημα.
, από το προηγούμενο υποερώτημα.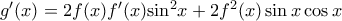 ή
ή  γιατί σύμφωνα με την υπόθεση
γιατί σύμφωνα με την υπόθεση 
 είναι σταθερή στο
είναι σταθερή στο  ώστε
ώστε  στο
στο  επομένως
επομένως  αφού
αφού 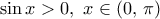 και ακόμη επειδή από την ισότητα επίσης
και ακόμη επειδή από την ισότητα επίσης  και συνεχής
και συνεχής  έτσι και
έτσι και  , επομένως
, επομένως 
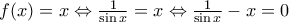 έχει ακριβώς δύο ρίζες στο διάστημα
έχει ακριβώς δύο ρίζες στο διάστημα  .
.  που είναι συνεχής με
που είναι συνεχής με  άρα υπάρχει
άρα υπάρχει  και
και  και με
και με  άρα υπάρχει
άρα υπάρχει 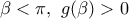 επομένως
επομένως  και σύμφωνα με το θεώρημα του Bolzano
και σύμφωνα με το θεώρημα του Bolzano  ώστε
ώστε  .
. έχει τρείς ρίζες
έχει τρείς ρίζες 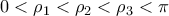 τότε στα διαστήματα
τότε στα διαστήματα ![[{{\rho }_{1}},\,{{\rho }_{2}}],\,\,\,[{{\rho }_{2}},\,{{\rho }_{3}}] [{{\rho }_{1}},\,{{\rho }_{2}}],\,\,\,[{{\rho }_{2}},\,{{\rho }_{3}}]](/forum/ext/geomar/texintegr/latexrender/pictures/40faac26a31e7c8c45161ea1d72dfdce.png) αφού η
αφού η  παραγωγίσιμη με
παραγωγίσιμη με 
 θα έχει δύο ρίζες στο
θα έχει δύο ρίζες στο  που είναι άτοπο γιατι
που είναι άτοπο γιατι  οπότε η
οπότε η  γνήσια αύξουσα άρα και
γνήσια αύξουσα άρα και 
 και
και  άρα η
άρα η  και
και ![[{{x}_{1}},\frac{{{x}_{1}}+{{x}_{2}}}{2}],\,\,[\frac{{{x}_{1}}+{{x}_{2}}}{2},\,{{x}_{2}}] [{{x}_{1}},\frac{{{x}_{1}}+{{x}_{2}}}{2}],\,\,[\frac{{{x}_{1}}+{{x}_{2}}}{2},\,{{x}_{2}}]](/forum/ext/geomar/texintegr/latexrender/pictures/bea7b2355adc4429f5fd1c18405f819d.png)
 προκύπτει ότι
προκύπτει ότι  και επειδή από (β)
και επειδή από (β)  ισχύει ότι
ισχύει ότι 