Δίνεται η συνάρτηση

α) Να μελετηθεί η
 ως προς τη μονοτονία και τα ακρότατα
ως προς τη μονοτονία και τα ακρόταταβ) i) Να βρεθεί η εξίσωση της εφαπτομένης της γραφικής παράστασης της
 στο
στο 
ii) να λυθεί η εξίσωση

γ) Να δείξετε ότι

Συντονιστής: Καρδαμίτσης Σπύρος

 ως προς τη μονοτονία και τα ακρότατα
ως προς τη μονοτονία και τα ακρότατα στο
στο 


 η
η 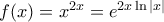 με
με  άρα συνεχής και στο
άρα συνεχής και στο 
 παραγωγίσιμη με
παραγωγίσιμη με  και τότε
και τότε 


 είναι γνήσια αύξουσα στα διαστήματα
είναι γνήσια αύξουσα στα διαστήματα ![(-\infty ,\,-\frac{1}{e}],\,\,[\frac{1}{e},\,+\infty ) (-\infty ,\,-\frac{1}{e}],\,\,[\frac{1}{e},\,+\infty )](/forum/ext/geomar/texintegr/latexrender/pictures/f102db8dc798e590770e13ae70484fd5.png) και γνήσια φθίνουσα στο διάστημα
και γνήσια φθίνουσα στο διάστημα ![[-\frac{1}{e},\,\,\frac{1}{e}] [-\frac{1}{e},\,\,\frac{1}{e}]](/forum/ext/geomar/texintegr/latexrender/pictures/18023b1b560c8f18a306d75f5b8265ba.png) άρα έχει τοπικό μέγιστο το
άρα έχει τοπικό μέγιστο το  και τοπικό μέγιστο το
και τοπικό μέγιστο το 
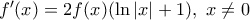 άρα
άρα  και η εφαπτομένη τότε είναι
και η εφαπτομένη τότε είναι 
 έχει προφανή ρίζα την
έχει προφανή ρίζα την  και τώρα η συνάρτηση
και τώρα η συνάρτηση 
 γιατί για
γιατί για  η
η  και
και 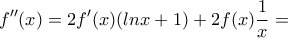

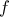 κυρτή και λόγω κυρτότητας ισχύει
κυρτή και λόγω κυρτότητας ισχύει  και
και  άρα η εξίσωση έχει μοναδική ρίζα την
άρα η εξίσωση έχει μοναδική ρίζα την 
![\begin{array}{*{20}{l}}
{\left. {\begin{array}{*{20}{l}}
{f\left( x \right) \ge 2x - 1\mathop \Rightarrow \limits^{x \ge 0} f\left( {x + 1} \right) \ge 2x + 1\mathop \Rightarrow \limits^{x \ge 0} xf\left( {x + 1} \right) \ge 2{x^2} + x \Rightarrow \int\limits_0^1 {xf\left( {x + 1} \right)} {\mkern 1mu} dx > \left[ {\frac{2}{3}{x^3} + \frac{1}{2}{x^2}} \right]_0^1}\\
{f\left( x \right) \ge 2x - 1\mathop \Rightarrow \limits^{1 \ge x \ge 0} \left( {x - 1} \right)f\left( x \right) \le \left( {x - 1} \right)\left( {2x - 1} \right)\mathop \Rightarrow \limits^{x \ge 0} \int\limits_0^1 {\left( {x - 1} \right)f\left( x \right)} {\mkern 1mu} dx < \left[ {\frac{2}{3}{x^3} - \frac{3}{2}{x^2} + x} \right]_0^1 \Rightarrow }
\end{array}} \right\} \Rightarrow }\\
{\left. {\begin{array}{*{20}{l}}
{\int\limits_0^1 {xf\left( {x + 1} \right)} {\mkern 1mu} dx > \left[ {\frac{2}{3}{x^3} + \frac{1}{2}{x^2}} \right]_0^1}\\
{ - \int\limits_0^1 {\left( {x - 1} \right)f\left( x \right)} {\mkern 1mu} dx > - \left[ {\frac{2}{3}{x^3} - \frac{3}{2}{x^2} + x} \right]_0^1}
\end{array}} \right\} \Rightarrow \int\limits_0^1 {xf\left( {x + 1} \right)} {\mkern 1mu} dx - \int\limits_0^1 {\left( {x - 1} \right)f\left( x \right)} {\mkern 1mu} dx > \left[ {2{x^2} - x} \right]_0^1 = 1}
\end{array} \begin{array}{*{20}{l}}
{\left. {\begin{array}{*{20}{l}}
{f\left( x \right) \ge 2x - 1\mathop \Rightarrow \limits^{x \ge 0} f\left( {x + 1} \right) \ge 2x + 1\mathop \Rightarrow \limits^{x \ge 0} xf\left( {x + 1} \right) \ge 2{x^2} + x \Rightarrow \int\limits_0^1 {xf\left( {x + 1} \right)} {\mkern 1mu} dx > \left[ {\frac{2}{3}{x^3} + \frac{1}{2}{x^2}} \right]_0^1}\\
{f\left( x \right) \ge 2x - 1\mathop \Rightarrow \limits^{1 \ge x \ge 0} \left( {x - 1} \right)f\left( x \right) \le \left( {x - 1} \right)\left( {2x - 1} \right)\mathop \Rightarrow \limits^{x \ge 0} \int\limits_0^1 {\left( {x - 1} \right)f\left( x \right)} {\mkern 1mu} dx < \left[ {\frac{2}{3}{x^3} - \frac{3}{2}{x^2} + x} \right]_0^1 \Rightarrow }
\end{array}} \right\} \Rightarrow }\\
{\left. {\begin{array}{*{20}{l}}
{\int\limits_0^1 {xf\left( {x + 1} \right)} {\mkern 1mu} dx > \left[ {\frac{2}{3}{x^3} + \frac{1}{2}{x^2}} \right]_0^1}\\
{ - \int\limits_0^1 {\left( {x - 1} \right)f\left( x \right)} {\mkern 1mu} dx > - \left[ {\frac{2}{3}{x^3} - \frac{3}{2}{x^2} + x} \right]_0^1}
\end{array}} \right\} \Rightarrow \int\limits_0^1 {xf\left( {x + 1} \right)} {\mkern 1mu} dx - \int\limits_0^1 {\left( {x - 1} \right)f\left( x \right)} {\mkern 1mu} dx > \left[ {2{x^2} - x} \right]_0^1 = 1}
\end{array}](/forum/ext/geomar/texintegr/latexrender/pictures/0caddfd6df27c26363f16211662c0fdb.png)
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 5 επισκέπτες