 για την οποία γνωρίζουμε ότι
για την οποία γνωρίζουμε ότι για κάθε
για κάθε  πραγματικούς με
πραγματικούς με  (1)
(1) (2
(2α) Να δείξετε ότι η
 είναι περιττή
είναι περιττήβ) Να δείξετε ότι η
 είναι παραγωγίσιμη με
είναι παραγωγίσιμη με  ,
,  πραγματικό
πραγματικόγ) Να λυθεί η εξίσωση

δ) Να μελετηθεί η
 ως προς τα κοίλα και να δείξετε ότι
ως προς τα κοίλα και να δείξετε ότι 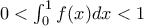
Συντονιστής: Καρδαμίτσης Σπύρος
 για την οποία γνωρίζουμε ότι
για την οποία γνωρίζουμε ότι για κάθε
για κάθε  πραγματικούς με
πραγματικούς με  (1)
(1) (2
(2 είναι περιττή
είναι περιττή είναι παραγωγίσιμη με
είναι παραγωγίσιμη με  ,
,  πραγματικό
πραγματικό
 ως προς τα κοίλα και να δείξετε ότι
ως προς τα κοίλα και να δείξετε ότι 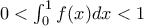
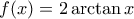 (εδώ
(εδώ  είναι η αντίστροφη της
είναι η αντίστροφη της  ).
).  . Και λοιπά.
. Και λοιπά.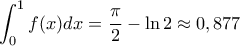
...για την παρέα...
 το
το  προκύπτει ότι
προκύπτει ότι  και με όπου
και με όπου  το
το  προκύπτει
προκύπτει 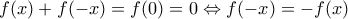 επομένως η
επομένως η  είναι περιττή.
είναι περιττή.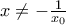 το
το 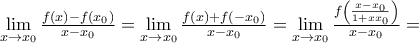
 γιατί
γιατί 
 άρα η
άρα η  είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  με
με  .
.



 (1) και τώρα για την συνάρτηση
(1) και τώρα για την συνάρτηση  ισχύει ότι
ισχύει ότι 
 είναι γνήσια φθίνουσα άρα και
είναι γνήσια φθίνουσα άρα και  και έτσι η (1) ισοδύναμα γίνεται
και έτσι η (1) ισοδύναμα γίνεται 
 οπότε είναι
οπότε είναι  άρα κοίλη στο
άρα κοίλη στο  και
και 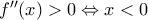 άρα κυρτή στο
άρα κυρτή στο ![(-\infty ,\,\,0] (-\infty ,\,\,0]](/forum/ext/geomar/texintegr/latexrender/pictures/cd17cf06f26e60f04a61cbb7ad9ef856.png)
 είναι γνήσια αύξουσα στο
είναι γνήσια αύξουσα στο  ισχύει για
ισχύει για  και επειδή
και επειδή  κοίλη στο
κοίλη στο  θα είναι κάτω εκτός του σημείου επαφής από κάθε εφαπτομένη της άρα και αυτής στο σημείο της
θα είναι κάτω εκτός του σημείου επαφής από κάθε εφαπτομένη της άρα και αυτής στο σημείο της 
 και θα ισχύει ότι
και θα ισχύει ότι  οπότε
οπότε 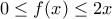

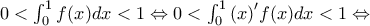
![\Leftrightarrow 0<\left[ xf(x) \right]_{0}^{1}-\int_{0}^{1}{x\frac{2}{{{x}^{2}}+1}}dx<1\Leftrightarrow 0<f(1)-\int_{0}^{1}{\frac{2x}{{{x}^{2}}+1}}dx<1 \Leftrightarrow 0<\left[ xf(x) \right]_{0}^{1}-\int_{0}^{1}{x\frac{2}{{{x}^{2}}+1}}dx<1\Leftrightarrow 0<f(1)-\int_{0}^{1}{\frac{2x}{{{x}^{2}}+1}}dx<1](/forum/ext/geomar/texintegr/latexrender/pictures/a7500662d116d49e1925f282ec7c88f9.png)
![\displaystyle 0<f(1)-\int_{0}^{1}{{{\left( \ln ({{x}^{2}}+1) \right)}^{\prime }}}dx<1\Leftrightarrow 0<f(1)-\left[ \ln ({{x}^{2}}+1) \right]_{0}^{1}dx<1\Leftrightarrow \displaystyle 0<f(1)-\int_{0}^{1}{{{\left( \ln ({{x}^{2}}+1) \right)}^{\prime }}}dx<1\Leftrightarrow 0<f(1)-\left[ \ln ({{x}^{2}}+1) \right]_{0}^{1}dx<1\Leftrightarrow](/forum/ext/geomar/texintegr/latexrender/pictures/137c237ab05a15edde60dd81ff549fb6.png)
 (2)
(2)  και ακόμη
και ακόμη 

![\left[ f(\varepsilon \phi x) \right]_{0}^{\frac{\pi }{4}}=\frac{\pi }{2}\Leftrightarrow f(\varepsilon \phi \frac{\pi }{4})-f(0)=\frac{\pi }{2}\Leftrightarrow f(1)=\frac{\pi }{2} \left[ f(\varepsilon \phi x) \right]_{0}^{\frac{\pi }{4}}=\frac{\pi }{2}\Leftrightarrow f(\varepsilon \phi \frac{\pi }{4})-f(0)=\frac{\pi }{2}\Leftrightarrow f(1)=\frac{\pi }{2}](/forum/ext/geomar/texintegr/latexrender/pictures/442c6aada5f3b49e352e08cdde563eac.png) έτσι από (2) θέλουμε
έτσι από (2) θέλουμε  που ισχύει.
που ισχύει.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες