M.S.Vovos έγραψε: ↑Τρί Μαρ 26, 2019 10:14 pm
Πολύ κλασική άσκηση αλλά αφού μπαίνουμε σιγά σιγά σε επαναλήψεις είπα να την ανεβάσω.
Δίνεται η συνάρτηση

με

και:
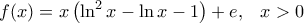 (α)
(α) Να εξετάσετε αν η

είναι συνεχής και παραγωγίσιμη.
(β) Να μελετήσετε την

ως προς τη μονοτονία, τα ακρότατα και το σύνολο τιμών της.
(γ) Να μελετήσετε την

ως προς την κυρτότητα και τις ασύμπτωτες της.
(δ) Να κάνετε μια πρόχειρη γραφική παράσταση της

, σε ορθοκανονικό σύστημα συντεταγμένων.
(ε) Να προσδιορίσετε το πλήθος των λύσεων της εξίσωσης

,

για τις διάφορες τιμές του πραγματικού αριθμού

, χρησιμοποιώντας το γράφημα που κάνατε στο ερώτημα (δ'). Να επαληθεύσετε τα αποτελέσματα που βρήκατε, δίνοντας πλήρη απόδειξη.
Φιλικά,
Μάριος
Αφού μπήκαμε σε κλίμα επανάληψης , πάμε σιγά σιγά.. !! Ας θυμόμαστε και τίποτα μιας και πλέον δεν ασχολούμαι με το κλάδο οπότε πολλά τα έχω ξεχάσει.
(α) Η

που μας δίδεται γράφεται ως:

Είναι προφανές ότι η

είναι συνεχής στο

ως γινόμενο συνεχών συναρτήσεων. Επιπλέον η

είναι συνεχής στο

αφού

, διότι γενικά ισχύει

όπου

. ( απλό και γνωστό και βγαίνει π.χ με DLH ) Άρα η

είναι συνεχής στο

.
Στο

η

είναι παραγωγίσιμη ως πράξεις παραγωγίσιμων με παράγωγο

. Θα ελέγξουμε τη παραγωγισιμότητα της

στο

. Από τον ορισμό της παραγώγου έχουμε:

Συνεπώς η

δεν είναι παραγωγίσιμη στο

.
(β ,γ) Στο

η

είναι παραγωγίσιμη με παράγωγο

και η

είναι ξανά παραγωγίσιμη με παράγωγο

. Στο παρακάτω πίνακα φαίνεται η μονοτονία της

, τα σημεία καμπής καθώς επίσης και τα ακρότατα.

- quicklatex.com-4b3e1702ee5010d9552023e38c58bf78_l3.png (6.11 KiB) Προβλήθηκε 1307 φορές
Συνεπώς η

παρουσιάζει στο

τοπικό μέγιστο ενώ στο

τοπικό ελάχιστο και στο και

ολικό ελάχιστο.Στο σημείο

παρουσιάζει σημείο καμπής. Από τον πίνακα φαίνεται επιπλέον ότι η

είναι κυρτή στο διάστημα

και κοίλη στο
![\left [0, \frac{1}{\sqrt{e}} \right ] \left [0, \frac{1}{\sqrt{e}} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/b56e3f38d9623be15c6a843def8869cb.png)
ενώ είναι γνήσια φθίνουσα στα διαστήματα
![\left [ \frac{1}{e^2}, \frac{1}{\sqrt{e}} \right ] \; , \; \left [ \frac{1}{\sqrt{e}} , e \right ] \left [ \frac{1}{e^2}, \frac{1}{\sqrt{e}} \right ] \; , \; \left [ \frac{1}{\sqrt{e}} , e \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/3cdb4b31c273c323bbb8442e605a7ada.png)
και γνήσια αύξουσα στα διαστήματα
![\left [ 0, \frac{1}{e^2} \right ] \; , \; \left [ e, +\infty \right ) \left [ 0, \frac{1}{e^2} \right ] \; , \; \left [ e, +\infty \right )](/forum/ext/geomar/texintegr/latexrender/pictures/091d078cfba22ae5f6788d4b54d9c7b2.png)
. Tο σύνολο τιμών της

είναι το σύνολο
![\displaystyle{\Delta = \left [ f(0), f \left ( \frac{1}{e^2} \right ) \right ] \cup \left [ f(e) , \lim_{x\rightarrow +\infty} f(x) \right ) = \left [ e, e + \frac{5}{e^2} \right ] \cup \left [ 0, +\infty \right ) = \left [ 0, +\infty \right )} \displaystyle{\Delta = \left [ f(0), f \left ( \frac{1}{e^2} \right ) \right ] \cup \left [ f(e) , \lim_{x\rightarrow +\infty} f(x) \right ) = \left [ e, e + \frac{5}{e^2} \right ] \cup \left [ 0, +\infty \right ) = \left [ 0, +\infty \right )}](/forum/ext/geomar/texintegr/latexrender/pictures/f86ad7686b284d3aa1f21c547ef5e4c9.png)
αφού τετριμμένα είναι

.
Κατακόρυφες ασύμπτωτες προφανώς δεν υπάρχουν αφού η

είναι συνεχής σε όλο το πεδίο ορισμού. Θα αναζητήσουμε πλάγιες διότι

άρα δεν έχει οριζόντιες ασύμπτωτες η γραφική παράσταση της

. Αλλά δεν έχει ούτε πλάγιες αφού
![\displaystyle{ \begin{aligned}
\lim_{x\rightarrow +\infty} \frac{f(x)}{x} &= \lim_{x\rightarrow +\infty} \frac{x \left ( \ln^2 x - \ln x -1 \right )+e}{x}\\
&=\lim_{x\rightarrow +\infty} \left ( \ln^2 x - \ln x - 1 + \frac{e}{x} \right ) \\
&= \lim_{x\rightarrow +\infty} \left ( \ln^2 x - \ln x - 1 \right ) + \lim_{x\rightarrow +\infty} \frac{e}{x}\\
&= \lim_{x\rightarrow +\infty} \left [ \ln x \left ( \ln x - 1 - \frac{1}{\ln x} \right ) \right ] + \lim_{x\rightarrow +\infty} \frac{e}{x} \\
&= +\infty
\end{aligned}} \displaystyle{ \begin{aligned}
\lim_{x\rightarrow +\infty} \frac{f(x)}{x} &= \lim_{x\rightarrow +\infty} \frac{x \left ( \ln^2 x - \ln x -1 \right )+e}{x}\\
&=\lim_{x\rightarrow +\infty} \left ( \ln^2 x - \ln x - 1 + \frac{e}{x} \right ) \\
&= \lim_{x\rightarrow +\infty} \left ( \ln^2 x - \ln x - 1 \right ) + \lim_{x\rightarrow +\infty} \frac{e}{x}\\
&= \lim_{x\rightarrow +\infty} \left [ \ln x \left ( \ln x - 1 - \frac{1}{\ln x} \right ) \right ] + \lim_{x\rightarrow +\infty} \frac{e}{x} \\
&= +\infty
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/b325abdb2451f4cc884b0229497d2bb2.png)
(δ) Η γραφική παράσταση φαίνεται παρακάτω:
![\displaystyle{\begin{tikzpicture}
\draw [->] (-0.5, 0) -- (5, 0) node[below]{x};
\draw [->] (0, -0.5) -- (0 , 5) node[left]{y};
\draw[blue, line width=2pt, domain=0.001:5.0,samples=100] plot[smooth](\x, {\x*( (ln(\x))^2 - ln(\x)-1) +2.72 });
\draw (-0.1, -0.2) node[left]{O};
\draw [fill=red] (0, 2.72) circle(2pt) ;
\draw (0, 2.72) node[left]{e};
\draw[fill=red] (2.72, 0) circle(2pt);
\draw (2.72, 0) node[below]{e};
\draw[fill=red] (0.1353, 3.3949) circle(2pt);
\draw[fill=red] (0.6065, 2.5666) circle(2pt);
\end{tikzpicture}} \displaystyle{\begin{tikzpicture}
\draw [->] (-0.5, 0) -- (5, 0) node[below]{x};
\draw [->] (0, -0.5) -- (0 , 5) node[left]{y};
\draw[blue, line width=2pt, domain=0.001:5.0,samples=100] plot[smooth](\x, {\x*( (ln(\x))^2 - ln(\x)-1) +2.72 });
\draw (-0.1, -0.2) node[left]{O};
\draw [fill=red] (0, 2.72) circle(2pt) ;
\draw (0, 2.72) node[left]{e};
\draw[fill=red] (2.72, 0) circle(2pt);
\draw (2.72, 0) node[below]{e};
\draw[fill=red] (0.1353, 3.3949) circle(2pt);
\draw[fill=red] (0.6065, 2.5666) circle(2pt);
\end{tikzpicture}}](/forum/ext/geomar/texintegr/latexrender/pictures/a910040e6c13379e18869149ca66229c.png)
(ε) Άμεσο από το σχήμα. Η αλγεβρική / αναλυτική απόδειξη μπορεί να περιμένει.
Θέμα Β; Σε καμία περίπτωση!! Είναι πολύ φορτωμένο! με
με  και:
και: 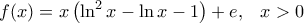
 είναι συνεχής και παραγωγίσιμη.
είναι συνεχής και παραγωγίσιμη. ως προς τη μονοτονία, τα ακρότατα και το σύνολο τιμών της.
ως προς τη μονοτονία, τα ακρότατα και το σύνολο τιμών της. ως προς την κυρτότητα και τις ασύμπτωτες της.
ως προς την κυρτότητα και τις ασύμπτωτες της. , σε ορθοκανονικό σύστημα συντεταγμένων.
, σε ορθοκανονικό σύστημα συντεταγμένων. ,
,  για τις διάφορες τιμές του πραγματικού αριθμού
για τις διάφορες τιμές του πραγματικού αριθμού  , χρησιμοποιώντας το γράφημα που κάνατε στο ερώτημα (δ'). Να επαληθεύσετε τα αποτελέσματα που βρήκατε, δίνοντας πλήρη απόδειξη.
, χρησιμοποιώντας το γράφημα που κάνατε στο ερώτημα (δ'). Να επαληθεύσετε τα αποτελέσματα που βρήκατε, δίνοντας πλήρη απόδειξη.

 ως γινόμενο συνεχών συναρτήσεων. Επιπλέον η
ως γινόμενο συνεχών συναρτήσεων. Επιπλέον η  αφού
αφού  , διότι γενικά ισχύει
, διότι γενικά ισχύει  όπου
όπου  . ( απλό και γνωστό και βγαίνει π.χ με DLH ) Άρα η
. ( απλό και γνωστό και βγαίνει π.χ με DLH ) Άρα η  .
. . Θα ελέγξουμε τη παραγωγισιμότητα της
. Θα ελέγξουμε τη παραγωγισιμότητα της 
 .
. και η
και η  είναι ξανά παραγωγίσιμη με παράγωγο
είναι ξανά παραγωγίσιμη με παράγωγο  . Στο παρακάτω πίνακα φαίνεται η μονοτονία της
. Στο παρακάτω πίνακα φαίνεται η μονοτονία της  τοπικό μέγιστο ενώ στο
τοπικό μέγιστο ενώ στο  ολικό ελάχιστο.Στο σημείο
ολικό ελάχιστο.Στο σημείο  παρουσιάζει σημείο καμπής. Από τον πίνακα φαίνεται επιπλέον ότι η
παρουσιάζει σημείο καμπής. Από τον πίνακα φαίνεται επιπλέον ότι η  και κοίλη στο
και κοίλη στο ![\left [0, \frac{1}{\sqrt{e}} \right ] \left [0, \frac{1}{\sqrt{e}} \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/b56e3f38d9623be15c6a843def8869cb.png) ενώ είναι γνήσια φθίνουσα στα διαστήματα
ενώ είναι γνήσια φθίνουσα στα διαστήματα ![\left [ \frac{1}{e^2}, \frac{1}{\sqrt{e}} \right ] \; , \; \left [ \frac{1}{\sqrt{e}} , e \right ] \left [ \frac{1}{e^2}, \frac{1}{\sqrt{e}} \right ] \; , \; \left [ \frac{1}{\sqrt{e}} , e \right ]](/forum/ext/geomar/texintegr/latexrender/pictures/3cdb4b31c273c323bbb8442e605a7ada.png) και γνήσια αύξουσα στα διαστήματα
και γνήσια αύξουσα στα διαστήματα ![\left [ 0, \frac{1}{e^2} \right ] \; , \; \left [ e, +\infty \right ) \left [ 0, \frac{1}{e^2} \right ] \; , \; \left [ e, +\infty \right )](/forum/ext/geomar/texintegr/latexrender/pictures/091d078cfba22ae5f6788d4b54d9c7b2.png) . Tο σύνολο τιμών της
. Tο σύνολο τιμών της ![\displaystyle{\Delta = \left [ f(0), f \left ( \frac{1}{e^2} \right ) \right ] \cup \left [ f(e) , \lim_{x\rightarrow +\infty} f(x) \right ) = \left [ e, e + \frac{5}{e^2} \right ] \cup \left [ 0, +\infty \right ) = \left [ 0, +\infty \right )} \displaystyle{\Delta = \left [ f(0), f \left ( \frac{1}{e^2} \right ) \right ] \cup \left [ f(e) , \lim_{x\rightarrow +\infty} f(x) \right ) = \left [ e, e + \frac{5}{e^2} \right ] \cup \left [ 0, +\infty \right ) = \left [ 0, +\infty \right )}](/forum/ext/geomar/texintegr/latexrender/pictures/f86ad7686b284d3aa1f21c547ef5e4c9.png)
 .
.![\displaystyle{ \begin{aligned}
\lim_{x\rightarrow +\infty} \frac{f(x)}{x} &= \lim_{x\rightarrow +\infty} \frac{x \left ( \ln^2 x - \ln x -1 \right )+e}{x}\\
&=\lim_{x\rightarrow +\infty} \left ( \ln^2 x - \ln x - 1 + \frac{e}{x} \right ) \\
&= \lim_{x\rightarrow +\infty} \left ( \ln^2 x - \ln x - 1 \right ) + \lim_{x\rightarrow +\infty} \frac{e}{x}\\
&= \lim_{x\rightarrow +\infty} \left [ \ln x \left ( \ln x - 1 - \frac{1}{\ln x} \right ) \right ] + \lim_{x\rightarrow +\infty} \frac{e}{x} \\
&= +\infty
\end{aligned}} \displaystyle{ \begin{aligned}
\lim_{x\rightarrow +\infty} \frac{f(x)}{x} &= \lim_{x\rightarrow +\infty} \frac{x \left ( \ln^2 x - \ln x -1 \right )+e}{x}\\
&=\lim_{x\rightarrow +\infty} \left ( \ln^2 x - \ln x - 1 + \frac{e}{x} \right ) \\
&= \lim_{x\rightarrow +\infty} \left ( \ln^2 x - \ln x - 1 \right ) + \lim_{x\rightarrow +\infty} \frac{e}{x}\\
&= \lim_{x\rightarrow +\infty} \left [ \ln x \left ( \ln x - 1 - \frac{1}{\ln x} \right ) \right ] + \lim_{x\rightarrow +\infty} \frac{e}{x} \\
&= +\infty
\end{aligned}}](/forum/ext/geomar/texintegr/latexrender/pictures/b325abdb2451f4cc884b0229497d2bb2.png)
![\displaystyle{\begin{tikzpicture}
\draw [->] (-0.5, 0) -- (5, 0) node[below]{x};
\draw [->] (0, -0.5) -- (0 , 5) node[left]{y};
\draw[blue, line width=2pt, domain=0.001:5.0,samples=100] plot[smooth](\x, {\x*( (ln(\x))^2 - ln(\x)-1) +2.72 });
\draw (-0.1, -0.2) node[left]{O};
\draw [fill=red] (0, 2.72) circle(2pt) ;
\draw (0, 2.72) node[left]{e};
\draw[fill=red] (2.72, 0) circle(2pt);
\draw (2.72, 0) node[below]{e};
\draw[fill=red] (0.1353, 3.3949) circle(2pt);
\draw[fill=red] (0.6065, 2.5666) circle(2pt);
\end{tikzpicture}} \displaystyle{\begin{tikzpicture}
\draw [->] (-0.5, 0) -- (5, 0) node[below]{x};
\draw [->] (0, -0.5) -- (0 , 5) node[left]{y};
\draw[blue, line width=2pt, domain=0.001:5.0,samples=100] plot[smooth](\x, {\x*( (ln(\x))^2 - ln(\x)-1) +2.72 });
\draw (-0.1, -0.2) node[left]{O};
\draw [fill=red] (0, 2.72) circle(2pt) ;
\draw (0, 2.72) node[left]{e};
\draw[fill=red] (2.72, 0) circle(2pt);
\draw (2.72, 0) node[below]{e};
\draw[fill=red] (0.1353, 3.3949) circle(2pt);
\draw[fill=red] (0.6065, 2.5666) circle(2pt);
\end{tikzpicture}}](/forum/ext/geomar/texintegr/latexrender/pictures/a910040e6c13379e18869149ca66229c.png)
