Αναρτώ ένα θέμα από τη συλλογή αυτή. Ας αφήσουμε ένα περιθώριο 2 ημερών στους μαθητές (έως την 25 Μαρτίου).
Δίνεται η συνάρτηση

Ε1. Να βρείτε το πεδίο ορισμού της και να αποδείξετε ότι η
 είναι άρτια συνάρτηση.
είναι άρτια συνάρτηση.Ε2. Να αποδείξετε ότι οι εφαπτόμενες της
 στα σημεία τομής της με τον άξονα
στα σημεία τομής της με τον άξονα  τέμνονται σε σημείο του άξονα
τέμνονται σε σημείο του άξονα  .
.Ε3. Να μελετήσετε την f ως προς τη μονοτονία, τα ακρότατα και την κυρτότητα.
Ε4. Να βρείτε τη μικρότερη τιμή του
 για την οποία ισχύει
για την οποία ισχύει για κάθε
για κάθε 
Ε5. Να παραστήσετε γραφικά τη συνάρτηση f. Στη συνέχεια να αποδείξετε ότι στο χωρίο που περικλείεται από την
 και τον άξονα
και τον άξονα  εγγράφεται μοναδικό τετράγωνο, οι δύο κορυφές του οποίου είναι σημεία της
εγγράφεται μοναδικό τετράγωνο, οι δύο κορυφές του οποίου είναι σημεία της  συμμετρικά ως προς τον άξονα
συμμετρικά ως προς τον άξονα  , ενώ οι δύο άλλες κορυφές του είναι οι προβολές στον άξονα
, ενώ οι δύο άλλες κορυφές του είναι οι προβολές στον άξονα  των κορυφών του τετραγώνου που ανήκουν στην
των κορυφών του τετραγώνου που ανήκουν στην  .
.
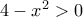 , απ'όπου εύκολα προκύπτει
, απ'όπου εύκολα προκύπτει  . Το
. Το  σύνολο συμμετρικό ως προς το 0 και για κάθε
σύνολο συμμετρικό ως προς το 0 και για κάθε  έχουμε
έχουμε  οπότε η
οπότε η  στα σημεία
στα σημεία  και
και 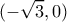 . Η
. Η 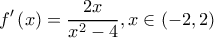 οπότε οι εφαπτομένες στα σημεία που αναφέρθηκαν είναι οι
οπότε οι εφαπτομένες στα σημεία που αναφέρθηκαν είναι οι  και
και 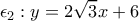 οι οποίες τέμνονται στο σημείο
οι οποίες τέμνονται στο σημείο  .
. για
για  και
και  για
για  . Λόγω συνέχειας στο 0, προκύπτει ότι η
. Λόγω συνέχειας στο 0, προκύπτει ότι η ![(-2,0] (-2,0]](/forum/ext/geomar/texintegr/latexrender/pictures/016c7eef578c235b770c667b8613a6b5.png) και γν. φθίνουσα στο
και γν. φθίνουσα στο  , ενώ παρουσιάζει (ολικό) μέγιστο στο
, ενώ παρουσιάζει (ολικό) μέγιστο στο  το
το  . 'Εχουμε ακόμα
. 'Εχουμε ακόμα  . Έπεται ότι η
. Έπεται ότι η  .
. ή ,ισοδύναμα,
ή ,ισοδύναμα,  με την ισότητα μονο για
με την ισότητα μονο για  . Επομένως πρέπει
. Επομένως πρέπει  ή ,ισοδύναμα,
ή ,ισοδύναμα,  . Άρα
. Άρα 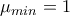 .
. και
και  και με βάση την κυρτότητα και την μονοτονία σχεδιάζουμε εύκολα.(Αφήνω το σχήμα στους ειδικούς του geogebra...)
και με βάση την κυρτότητα και την μονοτονία σχεδιάζουμε εύκολα.(Αφήνω το σχήμα στους ειδικούς του geogebra...) σημεία της
σημεία της  (η
(η  ) και τις προβολές αυτών πάνω στον
) και τις προβολές αυτών πάνω στον  , όπου
, όπου  (βρήκαμε τα σημεία τομής της
(βρήκαμε τα σημεία τομής της  . Πρέπει, λοιπόν, όλες οι σχηματιζόμενες πλευρές να είναι ίσες μεταξύ τους, δηλαδή πρέπει
. Πρέπει, λοιπόν, όλες οι σχηματιζόμενες πλευρές να είναι ίσες μεταξύ τους, δηλαδή πρέπει  ή ,ισοδύναμα,
ή ,ισοδύναμα, , καθώς προκύπτει ότι
, καθώς προκύπτει ότι  . Θεωρούμε την συνάρτηση
. Θεωρούμε την συνάρτηση ![g(x)=f(x)-x , x\in [0,\sqrt{3}] g(x)=f(x)-x , x\in [0,\sqrt{3}]](/forum/ext/geomar/texintegr/latexrender/pictures/e1098f357f69231397a1b3232a9d0ce5.png) η οποία είναι συνεχής και για την οποία
η οποία είναι συνεχής και για την οποία  και
και  . Από το Θ. Bolzano έπεται ότι υπάρχει μοναδικό
. Από το Θ. Bolzano έπεται ότι υπάρχει μοναδικό 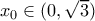 τέτοιο, ώστε
τέτοιο, ώστε  ή ,ισοδύναμα,
ή ,ισοδύναμα,![[-a, a], a>0 [-a, a], a>0](/forum/ext/geomar/texintegr/latexrender/pictures/f865e0494a7279cfef9021c90dfbc266.png) είτε τέμνονται πάνω στον κατακόρυφο άξονα
είτε τέμνονται πάνω στον κατακόρυφο άξονα 
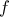 είναι παραγωγίσιμη και άρτια τότε η παράγωγός της είναι περιττή , αφού :
είναι παραγωγίσιμη και άρτια τότε η παράγωγός της είναι περιττή , αφού :
 είναι :
είναι :
 είναι :
είναι : 
 παίρνουμε και απ΄τις δύο ότι :
παίρνουμε και απ΄τις δύο ότι : 
 του άξονα
του άξονα 