
α) Να δείξετε ότι η
 είναι γνησίως αύξουσα.
είναι γνησίως αύξουσα. β) Να βρείτε το σύνολο τιμών της

γ) Να λύσετε την ανίσωση

δ) Να λύσετε την εξίσωση

ε) Να λύσετε την εξίσωση
 στο διάστημα
στο διάστημα 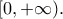
**ε') Να λύσετε την εξίσωση
 στο
στο 
Μια δική μου κατασκευή!
Συντονιστής: Καρδαμίτσης Σπύρος
Δείξε μας τι έχεις κάνει. Μια υπόδειξη, για μία λύση, εμπλέκει τρία Rolle και άτοπο. Βρες δηλαδή ποιες είναι με το μάτι οι ρίζες και απέρριψε να έχει άλλη η εξίσωση.
Αυτό που κατάλαβα είναι ότι πρέπει να δείξω ότι η
 είναι φθίνουσα και μετά αύξουσα άρα το πολύ 2 ρίζες οι 0,1 αλλά γίνεται χαμός με τις παραγώγους, το rolle το ξέρω πολύ επιφανειακά οπότε δε κατάλαβα πως με βοηθάει στο άτοπο. Αφήστε το όταν προχωρήσω λίγο θα το ξαναδώ τα υπόλοιπα όλα καλά
είναι φθίνουσα και μετά αύξουσα άρα το πολύ 2 ρίζες οι 0,1 αλλά γίνεται χαμός με τις παραγώγους, το rolle το ξέρω πολύ επιφανειακά οπότε δε κατάλαβα πως με βοηθάει στο άτοπο. Αφήστε το όταν προχωρήσω λίγο θα το ξαναδώ τα υπόλοιπα όλα καλάΌχι, δεν είναι καλή ιδέα οι παράγωγοι. Θα δώσω με απόκρυψη μία υπόδειξη χωρίς να χαλάω την άσκηση.4ptil έγραψε: ↑Πέμ Δεκ 31, 2020 4:00 pm
Αυτό που κατάλαβα είναι ότι πρέπει να δείξω ότι ηείναι φθίνουσα και μετά αύξουσα άρα το πολύ 2 ρίζες οι 0,1 αλλά γίνεται χαμός με τις παραγώγους, το rolle το ξέρω πολύ επιφανειακά οπότε δε κατάλαβα πως με βοηθάει στο άτοπο. Αφήστε το όταν προχωρήσω λίγο θα το ξαναδώ τα υπόλοιπα όλα καλά
Done!Mihalis_Lambrou έγραψε: ↑Πέμ Δεκ 31, 2020 4:14 pmΌχι, δεν είναι καλή ιδέα οι παράγωγοι. Θα δώσω με απόκρυψη μία υπόδειξη χωρίς να χαλάω την άσκηση.4ptil έγραψε: ↑Πέμ Δεκ 31, 2020 4:00 pm
Αυτό που κατάλαβα είναι ότι πρέπει να δείξω ότι ηείναι φθίνουσα και μετά αύξουσα άρα το πολύ 2 ρίζες οι 0,1 αλλά γίνεται χαμός με τις παραγώγους, το rolle το ξέρω πολύ επιφανειακά οπότε δε κατάλαβα πως με βοηθάει στο άτοπο. Αφήστε το όταν προχωρήσω λίγο θα το ξαναδώ τα υπόλοιπα όλα καλά
.
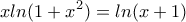
 τοτε
τοτε  αρα
αρα 

 επαληθεύει
επαληθεύει τοτ
τοτ  αρα
αρα 

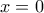 επαληθεύει
επαληθεύει τότε
τότε  αδυνατη
αδυνατη τοτε
τοτε  αδυνατη
αδυνατηΩραία! Ουσιαστικά έχουμε ότι η
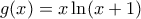 είναι γνήσια αύξουσα στο
είναι γνήσια αύξουσα στο  και
και 
Εδώ δεν έχουμε άτοπο (
 )!
)!Το ε) χωρίς παραγώγους, όπως το εννοούσα στο παραπάνω. Ουσιστικά είναι το ίδιο με του Ροδόλφου στο ποστ #Mihalis_Lambrou έγραψε: ↑Πέμ Δεκ 31, 2020 4:14 pm
Όχι, δεν είναι καλή ιδέα οι παράγωγοι. Θα δώσω με απόκρυψη μία υπόδειξη χωρίς να χαλάω την άσκηση.
.
α) Βρες δύο προφανείς ρίζες.
β) Δείξε ότι στο μεσοδιάστημα των δύο ριζών η μία συνάρτηση είναι προφανώς μεγαλύτερη από την άλλη (θα το δεις με το μάτι, χωρίς να παραγώγους), ενώ έξω από το διάστημα είναι προφανώς μικρότερη.
 αλλά χωρίς λογαρίθμους.
αλλά χωρίς λογαρίθμους. και
και  . Τώρα,
. Τώρα,  έχουμε
έχουμε  , άρα ποτέ ίσα. Όμοια
, άρα ποτέ ίσα. Όμοια  έχουμε
έχουμε  , άρα ποτέ ίσα.
, άρα ποτέ ίσα.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες