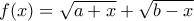
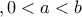
α) Μελετήστε την συνάρτηση ως προς την μονοτονία και τα ακρότατα .
β) Υπολογίστε το :
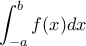 , στην περίπτωση που :
, στην περίπτωση που : 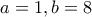 .
.Συντονιστής: Καρδαμίτσης Σπύρος
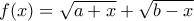
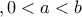
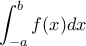 , στην περίπτωση που :
, στην περίπτωση που : 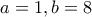 .
.α)
![\displaystyle {D_f} = [ - a,b] \displaystyle {D_f} = [ - a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/db6773fd8d34b0c56cde2d0d1153cd3a.png) και
και 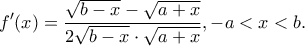
 είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο ![\displaystyle \left[ { - a,\frac{{b - a}}{2}} \right] \displaystyle \left[ { - a,\frac{{b - a}}{2}} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/dccb3235aed3264957c5a06b7b9577bb.png) και γνησίως
και γνησίως ![\displaystyle \left[ {\frac{{b - a}}{2},b} \right]. \displaystyle \left[ {\frac{{b - a}}{2},b} \right].](/forum/ext/geomar/texintegr/latexrender/pictures/d1c0ee49c7bd74107a2c9a5d870246b5.png) Στο
Στο 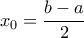 έχουμε ολικό μέγιστο ίσο με
έχουμε ολικό μέγιστο ίσο με 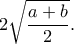 Έχουμε ακόμα ολικό
Έχουμε ακόμα ολικό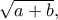 στα άκρα του πεδίου ορισμού
στα άκρα του πεδίου ορισμού  και
και 
![\displaystyle \int_{ - 1}^8 {f(x)dx = \frac{2}{3}\left[ {\sqrt {{{(1 + x)}^3}} - \sqrt {{{(8 - x)}^3}} } \right]} _{ - 1}^8 = 36 \displaystyle \int_{ - 1}^8 {f(x)dx = \frac{2}{3}\left[ {\sqrt {{{(1 + x)}^3}} - \sqrt {{{(8 - x)}^3}} } \right]} _{ - 1}^8 = 36](/forum/ext/geomar/texintegr/latexrender/pictures/a62dbb4cb393617227581b34c7639c7a.png)
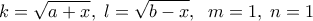 , για
, για ![\displaystyle x \in \left[ {a,b} \right] \displaystyle x \in \left[ {a,b} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/fab6c5e7befd1bc9b27f1da06df99d38.png)
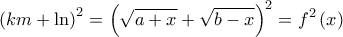
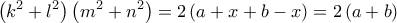
 είναι
είναι 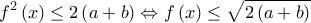 , αφού
, αφού 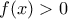 για κάθε
για κάθε ![\displaystyle x \in \left[ {a,b} \right] \displaystyle x \in \left[ {a,b} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/fab6c5e7befd1bc9b27f1da06df99d38.png) .
.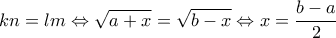
![\displaystyle x \in \left[ {a,b} \right] \displaystyle x \in \left[ {a,b} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/fab6c5e7befd1bc9b27f1da06df99d38.png) παίρνουμε
παίρνουμε 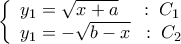
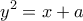 και τον αρνητικό κλάδο της
και τον αρνητικό κλάδο της 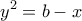 στο διάστημα
στο διάστημα ![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) .
. ![\displaystyle x = {x_0},\;\;{x_0} \in \left[ {a,b} \right] \displaystyle x = {x_0},\;\;{x_0} \in \left[ {a,b} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/bca7a54e0aa4ecc7dfd5e54721301c65.png) τέμνει τους κλάδους
τέμνει τους κλάδους 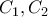 αντίστοιχα στα σημεία
αντίστοιχα στα σημεία 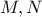 .
.  παριστάνει το άθροισμα των απολύτων των τεταγμένων των κλάδων της παραβολής, δηλαδή το άθροισμα
παριστάνει το άθροισμα των απολύτων των τεταγμένων των κλάδων της παραβολής, δηλαδή το άθροισμα 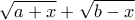 , με
, με ![\displaystyle x \in \left[ {a,b} \right] \displaystyle x \in \left[ {a,b} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/fab6c5e7befd1bc9b27f1da06df99d38.png) .
.![\displaystyle {f_1}\left( x \right) = \sqrt {a + x} \;\;\;\kappa \alpha \iota \;\;\;{f_2}\left( x \right) = - \sqrt {b - x} \;\;\;x \in \left[ {a,b} \right]. \displaystyle {f_1}\left( x \right) = \sqrt {a + x} \;\;\;\kappa \alpha \iota \;\;\;{f_2}\left( x \right) = - \sqrt {b - x} \;\;\;x \in \left[ {a,b} \right].](/forum/ext/geomar/texintegr/latexrender/pictures/9bbaa5da65fed63ca3fe008d250ee734.png)
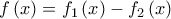 παρουσιάζει μέγιστο στο x0 και είναι παραγωγίσιμη στο
παρουσιάζει μέγιστο στο x0 και είναι παραγωγίσιμη στο  , θα είναι
, θα είναι 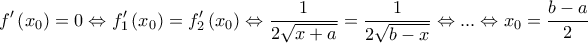
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 6 επισκέπτες