Μία παραγωγίσιμη συνάρτηση
Συντονιστής: Καρδαμίτσης Σπύρος
-
orestisgotsis
- Δημοσιεύσεις: 1753
- Εγγραφή: Σάβ Φεβ 25, 2012 10:19 pm
Μία παραγωγίσιμη συνάρτηση
ΠΕΡΙΤΤΑ
τελευταία επεξεργασία από orestisgotsis σε Παρ Φεβ 23, 2024 3:39 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Λέξεις Κλειδιά:
Re: Μία παραγωγίσιμη συνάρτηση
orestisgotsis έγραψε: ↑Πέμ Δεκ 14, 2023 10:25 pmΜια συνάρτησηείναι ορισμένη και συνεχής στο διάστημα:
, παραγωγίσιμη
στοκαι ισχύουν:
και
.
Να αποδείξετε ότι υπάρχει αριθμόςμε
.
- Αν
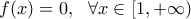 ,
,
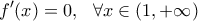
- Αν υπάρχει
 τέτοιο ώστε
τέτοιο ώστε 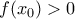 ,
,
 συνάρτηση
συνάρτηση 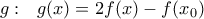 ισχύουν:
ισχύουν: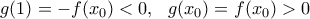 και εφόσον
και εφόσον 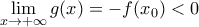 θα υπάρχει
θα υπάρχει  κοντά στο
κοντά στο  ,
, οπότε μπορούμε να επιλέξουμε
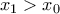 , τέτοιο ώστε:
, τέτοιο ώστε: 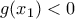
Από το Θεώρημα του Bolzano η
 έχει δύο ρίζες, μία στο
έχει δύο ρίζες, μία στο 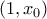 και μία στο
και μία στο 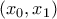
Από το Θεώρημα Rolle η
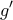 , μεταξύ των ριζών της
, μεταξύ των ριζών της  , θα έχει μία ρίζα.
, θα έχει μία ρίζα. Δηλαδή θα υπάρχει
 τέτοιο ώστε
τέτοιο ώστε 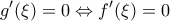
- Αν υπάρχει
 τέτοιο ώστε
τέτοιο ώστε 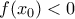 ,
,


-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15768
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Μία παραγωγίσιμη συνάρτηση
Ορίζουμεorestisgotsis έγραψε: ↑Πέμ Δεκ 14, 2023 10:25 pmΜια συνάρτησηείναι ορισμένη και συνεχής στο διάστημα:
, παραγωγίσιμη
στοκαι ισχύουν:
και
.
Να αποδείξετε ότι υπάρχει αριθμόςμε
.
![g:[0,\, 1] \longrightarrow \mathbb R g:[0,\, 1] \longrightarrow \mathbb R](/forum/ext/geomar/texintegr/latexrender/pictures/591810f0f2a770c29113361742a18f94.png) ως
ως 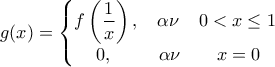
H
 είναι συνεχής στο
είναι συνεχής στο ![[0,\, 1] [0,\, 1]](/forum/ext/geomar/texintegr/latexrender/pictures/ef41a7200351813659470da746912f6e.png) και παραγωγίσιμη στο
και παραγωγίσιμη στο  (άμεσο) με
(άμεσο) με 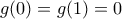 . Από Rolle υπάρχει
. Από Rolle υπάρχει 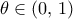 με
με 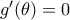 . Άρα
. Άρα 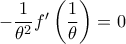 , από όπου
, από όπου 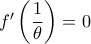 .
. Παίρνουμε τώρα
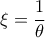 , που μας κάνει την δουλειά.
, που μας κάνει την δουλειά.-
orestisgotsis
- Δημοσιεύσεις: 1753
- Εγγραφή: Σάβ Φεβ 25, 2012 10:19 pm
Re: Μία παραγωγίσιμη συνάρτηση
ΠΕΡΙΤΤΑ
τελευταία επεξεργασία από orestisgotsis σε Παρ Φεβ 23, 2024 3:39 pm, έχει επεξεργασθεί 1 φορά συνολικά.
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15768
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Μία παραγωγίσιμη συνάρτηση
Mία λύση εκτός φακέλου (αλλά η οποία μπορεί να προσαρμοστεί να γίνει εντός φακέλου).orestisgotsis έγραψε: ↑Πέμ Δεκ 14, 2023 10:25 pmΜια συνάρτησηείναι ορισμένη και συνεχής στο διάστημα:
, παραγωγίσιμη
στοκαι ισχύουν:
και
.
Να αποδείξετε ότι υπάρχει αριθμόςμε
.
Δεν μπορεί για κάθε
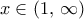 να ισχύει
να ισχύει 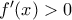 γιατί τότε η
γιατί τότε η  θα ήταν γνήσια αύξουσα οπότε θα είχαμε
θα ήταν γνήσια αύξουσα οπότε θα είχαμε 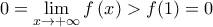 , άτοπο.
, άτοπο. Όμοια δεν μπορεί για κάθε
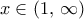 να ισχύει
να ισχύει 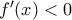 . Άρα υπάρχουν
. Άρα υπάρχουν 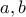 με
με 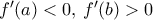 . Από Darboux, κάπου στο ενδιάμεσο θα μηδενίζεται η
. Από Darboux, κάπου στο ενδιάμεσο θα μηδενίζεται η  , όπως θέλαμε.
, όπως θέλαμε.-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15768
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Μία παραγωγίσιμη συνάρτηση
Αλλιώς: Ανorestisgotsis έγραψε: ↑Πέμ Δεκ 14, 2023 10:25 pmΜια συνάρτησηείναι ορισμένη και συνεχής στο διάστημα:
, παραγωγίσιμη
στοκαι ισχύουν:
και
.
Να αποδείξετε ότι υπάρχει αριθμόςμε
.
 σταθερά
σταθερά  , τελειώσαμε. Χωρίς βλάβη, λοιπόν, υπάρχει
, τελειώσαμε. Χωρίς βλάβη, λοιπόν, υπάρχει 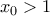 με
με 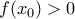 . Έστω
. Έστω  οποιοδήποτε με
οποιοδήποτε με 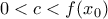 .
. Από ΘΕΤ υπάρχει
 με
με 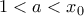 με
με 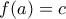 . Επίσης, επειδή
. Επίσης, επειδή 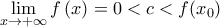 υπάρχει
υπάρχει  με
με 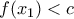 . Συνεπώς από ΘEΤ υπάρχει
. Συνεπώς από ΘEΤ υπάρχει 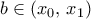 με
με 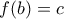 .
. Tέλος, αφού
 , από Rolle υπάρχει
, από Rolle υπάρχει 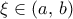 με
με  , όπως θέλαμε.
, όπως θέλαμε..
- Συνημμένα
-
- sinartisi sto apeiro.png (5.02 KiB) Προβλήθηκε 703 φορές
τελευταία επεξεργασία από Mihalis_Lambrou σε Κυρ Δεκ 17, 2023 11:04 pm, έχει επεξεργασθεί 1 φορά συνολικά.
Re: Μία παραγωγίσιμη συνάρτηση
Καλημέρα. Να το πω κάπως πιο απλά. Έστω ότιorestisgotsis έγραψε: ↑Πέμ Δεκ 14, 2023 10:25 pmΜια συνάρτησηείναι ορισμένη και συνεχής στο διάστημα:
, παραγωγίσιμη
στοκαι ισχύουν:
και
.
Να αποδείξετε ότι υπάρχει αριθμόςμε
.
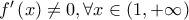 . Τότε, από τις συνέπειες του Θ. Darboux, η
. Τότε, από τις συνέπειες του Θ. Darboux, η  διατηρεί πρόσημο στο
διατηρεί πρόσημο στο 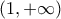 και αφού η
και αφού η  είναι συνεχής στο
είναι συνεχής στο 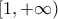 , η
, η  είναι γνησίως μονότονη στο
είναι γνησίως μονότονη στο 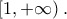 Αφού η
Αφού η  είναι συνεχής και γνησίως μονότονη στο
είναι συνεχής και γνησίως μονότονη στο 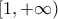 , έπεται ότι
, έπεται ότι 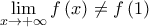 , άτοπο.
, άτοπο. Άρα, υπάρχει
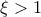 , τέτοιο ώστε
, τέτοιο ώστε 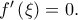
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15768
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Μία παραγωγίσιμη συνάρτηση
Καλώς ήλθες στο φόρουμ.
Αν δεις το ποστ #
 παραπάνω, θα διαπιστώσεις ότι η εκεί απόδειξη είναι ίδια με αυτήν που γράφεις.
παραπάνω, θα διαπιστώσεις ότι η εκεί απόδειξη είναι ίδια με αυτήν που γράφεις.Re: Μία παραγωγίσιμη συνάρτηση
Καλώς σας βρήκα.Mihalis_Lambrou έγραψε: ↑Κυρ Δεκ 17, 2023 10:07 amΚαλώς ήλθες στο φόρουμ.
Αν δεις το ποστ #παραπάνω, θα διαπιστώσεις ότι η εκεί απόδειξη είναι ίδια με αυτήν που γράφεις.
 στο
στο 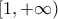 . Αν θέλετε, μπορώ να την σβήσω.
. Αν θέλετε, μπορώ να την σβήσω.-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15768
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Μία παραγωγίσιμη συνάρτηση
.
Δεν υπάρχει λόγος να σβήσεις το ποστ. Ίσα ίσα είναι χαρά μας να βλέπουμε ένα νέο μέλος να ασχολείται δυναμικά με τα τρέχοντα θέματα του φόρουμ.
Ας προσθέσω ότι στο ποστ μου δεν ανέφερα ότι η συνάρτηση είναι συνεχής επειδή είναι αυτονόητο. Επίσης, σημείωαα ότι η λύση μου είναι εκτός φακέλου, δηλαδή απευθύνεται στους συναδέλφους, που δεν έχουν ανάγκη της ρητής μνείας της συνέχειας. Παράλειψη μου, πάντως, και σωστά το επισημαίνεις.
-
Mihalis_Lambrou
- Επιμελητής
- Δημοσιεύσεις: 15768
- Εγγραφή: Κυρ Δεκ 21, 2008 2:04 am
Re: Μία παραγωγίσιμη συνάρτηση
Άλλη μία λύση: Ανorestisgotsis έγραψε: ↑Πέμ Δεκ 14, 2023 10:25 pmΜια συνάρτησηείναι ορισμένη και συνεχής στο διάστημα:
, παραγωγίσιμη
στοκαι ισχύουν:
και
.
Να αποδείξετε ότι υπάρχει αριθμόςμε
.
 η μηδενική συνάρτηση, τελειώσαμε. Αλλιώς, χωρίς βλάβη στην γενικότητα, η
η μηδενική συνάρτηση, τελειώσαμε. Αλλιώς, χωρίς βλάβη στην γενικότητα, η  λαμβάνει κάποια θετική τιμή, έστω
λαμβάνει κάποια θετική τιμή, έστω  . Εξετάζουμε τώρα την
. Εξετάζουμε τώρα την  σε διάστημα της μορφής
σε διάστημα της μορφής ![[1,\,a] [1,\,a]](/forum/ext/geomar/texintegr/latexrender/pictures/45314bec205aa5350d919b90c8667fd8.png) , όπου
, όπου 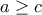 .
. Ξέρουμε από θεώρημα ότι η
 έχει ολικό μέγιστο στο
έχει ολικό μέγιστο στο ![[1,\,a] [1,\,a]](/forum/ext/geomar/texintegr/latexrender/pictures/45314bec205aa5350d919b90c8667fd8.png) . Ισχυρίζομαι ότι αν για κάθε
. Ισχυρίζομαι ότι αν για κάθε 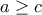 η
η  είχε το ολικό της μέγιστο στο δεξί άκρο του διαστήματος
είχε το ολικό της μέγιστο στο δεξί άκρο του διαστήματος ![[1,\, a] [1,\, a]](/forum/ext/geomar/texintegr/latexrender/pictures/da2aba4b261f22cc55aa109ca9c0d4ac.png) , τότε η συνάρτηση θα είναι αύξουσα. Πράγματι, έστω
, τότε η συνάρτηση θα είναι αύξουσα. Πράγματι, έστω 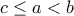 . Tότε
. Tότε 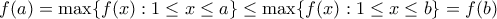 , όπως θέλαμε.
, όπως θέλαμε. Αλλά αυτό είναι άτοπο γιατί τότε για κάθε
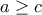 θα είχαμε
θα είχαμε 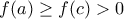 , και άρα δεν θα ίσχυε
, και άρα δεν θα ίσχυε 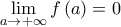 .
. Συμπέρασμα: Υπάρχει
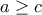 τέτοιο ώστε η
τέτοιο ώστε η  έχει ολικό μέγιστο σε εσωτερικό σημείο του
έχει ολικό μέγιστο σε εσωτερικό σημείο του ![[1, \, a] [1, \, a]](/forum/ext/geomar/texintegr/latexrender/pictures/269cdcfb1873e9d10ca9e9a0f977fb99.png) και άρα η παράγωγος
και άρα η παράγωγος  μηδενίζεται σε αυτό το σημείο, όπως θέλαμε να δείξουμε.
μηδενίζεται σε αυτό το σημείο, όπως θέλαμε να δείξουμε.Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 8 επισκέπτες
