Σε λίγο θα αρχίσει η προετοιμασία των παιδιών που θα δώσουν εξετάσεις του χρόνου τέτοια εποχή.
Έχοντας πλέον την επιμέλεια του φακέλου ΑΣΚΗΣΕΙΣ ΣΕ ΟΛΗ ΤΗΝ ΥΛΗ θα ήθελα να πούμε κάποια πράγματα για το φάκελλο αυτό.
Επειδή έχουμε όλο το χρόνο μπροστά μας μπορούμε να βρούμε ωραίες και περιεκτικές μικτές ασκήσεις ώστε να βοηθηθούμε όλοι στη προετοιμασία.
Θα παρακαλούσα οι προτεινόμενες ασκήσεις να είναι καλογραμμένες και οι λύσεις που θα δίνονται να είναι κάτι παραπάνω από πλήρεις.
Αυτές που είναι κατά τεκμήριο πολύ καλές, ουσιαστικές και χρήσιμες και που θα είναι πολλές, αφού τις επεξεργασθούμε θα τις συγκεντώνουμε και θα τις αξιοποιούμε έτσι ώστε τουλάχιστον όσοι προσφέρουν (είτε προτείνοντας είτε λύνοντας) τελικά να μπορούν και να τις αξιοποιήσουν. Το πως θα το βρούμε.
Υπάρχει περίπτωση κάποιες από αυτές να σας ζητηθούν να μου τις στείλεται γραμμένες σε word.
Αν κάποιο από τα θέματα που ήδη έχουν ζητηθεί και θεωρείται ότι πρέπει να ξανασυζητηθούν μπορείται να τα επαναφέρεται γιατί το ψάξιμο των αρχείων είναι πολύ επίπονη διαδικασία.
Νομίζω ότι όλοι οι καλοί φίλοι προπαρασκευαστές και όχι μόνον, θα φτιάξουμε έναν πολύ ωραίο χώρο αλληλοενημέρωσης και ουσιαστικής βοήθειας στη τόσο δύσκολη δουλειά μας.
Σαν αρχή ας δούμε ένα μικτό θέμα.
M.E.Θ 1 (Μικτό επαναληπτικό θέμα 1)
Δίνονται δυο μιγαδικοί αριθμοί
 , και η συνάρτηση f με τύπο
, και η συνάρτηση f με τύπο  ,
,  .
.i. Να βρεθεί το πεδίο ορισμού της συνάρτησης f.
ii. Να δειχθεί ότι η συνάρτηση f είναι 1-1.
iii. Να μελετηθεί η συνάρτηση f ως προς τη μονοτονία.
iv. Αν είναι γνωστό ότι η εξίσωση
 έχει μοναδική λύση, τότε:
έχει μοναδική λύση, τότε:1. να υπολογισθεί η διαφορά
 .
.2. Να αποδειχθεί ότι
 .
.Θωμάς





 ισοδυναμεί με την
ισοδυναμεί με την  οπότε
οπότε
 και
και που είναι δευτεροβάθμια και για να έχει μοναδική λύση πρέπει Δ=0 άρα
που είναι δευτεροβάθμια και για να έχει μοναδική λύση πρέπει Δ=0 άρα


 με
με 

 άρα f γνησίως αύξουσα, άρα και 1-1
άρα f γνησίως αύξουσα, άρα και 1-1
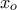 η μοναδική ρίζα, τότε
η μοναδική ρίζα, τότε 

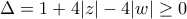
 ,
, 
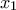 σίγουρα ικανοποιεί τη συνθήκη
σίγουρα ικανοποιεί τη συνθήκη  , άρα είναι η ζητούμενη ρίζα (
, άρα είναι η ζητούμενη ρίζα ( )
) πρέπει είτε να απορριφθεί είτε να ισχύει
πρέπει είτε να απορριφθεί είτε να ισχύει  (διπλή ρίζα), άρα
(διπλή ρίζα), άρα είτε β)
είτε β) 
 είτε β)
είτε β)
 έχω την άποψη ότι πρέπει στην
έχω την άποψη ότι πρέπει στην ,
, 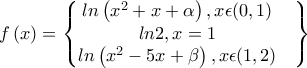 .
. και
και 
 και
και  να τελειώνουμε....ρε τι τράβαμε...τα "υπουργεία" μου μέσα
να τελειώνουμε....ρε τι τράβαμε...τα "υπουργεία" μου μέσα  έχουμε ότι:
έχουμε ότι:  .
. έχουμε ότι:
έχουμε ότι:  .
. είναι συνεχής στο 1 αν και μόνο αν
είναι συνεχής στο 1 αν και μόνο αν 
 .
. .
. .
. .
. .
. .
. .
. ,
, 
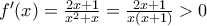 ,
,![(0,1] (0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/668c7b55a37300c330dcd565d9e076da.png) .
.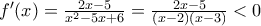 ,
, .
. το
το  .
. και
και  ,
, .
. και
και  ,
,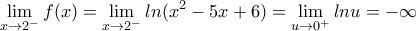 .
. στο οποίο η
στο οποίο η  .
. στο οποίο η
στο οποίο η ![\displaystyle{f(A_)=\left(\lim_{x\rightarrow 2^-},\lim_{x\rightarrow 1^+} \right]=(-\infty,ln2] \displaystyle{f(A_)=\left(\lim_{x\rightarrow 2^-},\lim_{x\rightarrow 1^+} \right]=(-\infty,ln2]](/forum/ext/geomar/texintegr/latexrender/pictures/894caf87b49a8ffd97d01a13fca64914.png) .
.![f(A)=f(A_1) \cup f(A_2)=(-\infty,ln2] f(A)=f(A_1) \cup f(A_2)=(-\infty,ln2]](/forum/ext/geomar/texintegr/latexrender/pictures/b62fda86118d39ad8b17ad0b53630ee4.png) .
.
 .
. , ενώ
, ενώ  ,
, .
. , οπότε απορρίπτεται,
, οπότε απορρίπτεται, , είναι δεκτή,
, είναι δεκτή,  .
. έχουμε ότι
έχουμε ότι  .
. .
. , απορρίπτεται,
, απορρίπτεται,  .
. , είναι δεκτή,
, είναι δεκτή,  .
. και
και  , οπότε οι ευθείες
, οπότε οι ευθείες  είναι κατακόρυφες ασύμπτωτες.
είναι κατακόρυφες ασύμπτωτες. δεν έχει πλάγιες ασύμπτωτες (δηλαδή, ούτε και οριζόντιες).
δεν έχει πλάγιες ασύμπτωτες (δηλαδή, ούτε και οριζόντιες).![\displaystyle{\int_{\frac{1}{2}}^{1} ln(x^2+x)dx=\int_{\frac{1}{2}}^{1}(x){'}ln(x^2+x)dx=\left[ xln(x^2+x)\right]_{\frac{1}{2}}^{1}-\int_{\frac{1}{2}}^{1} \frac{x(2x+1)}{x^2+x}dx=} \displaystyle{\int_{\frac{1}{2}}^{1} ln(x^2+x)dx=\int_{\frac{1}{2}}^{1}(x){'}ln(x^2+x)dx=\left[ xln(x^2+x)\right]_{\frac{1}{2}}^{1}-\int_{\frac{1}{2}}^{1} \frac{x(2x+1)}{x^2+x}dx=}](/forum/ext/geomar/texintegr/latexrender/pictures/290ba13aed16bc58efaf8b4dacbfd477.png)
![\displaystyle{=\left[ xln(x^2+x)\right]_{\frac{1}{2}}^{1}-\int_{\frac{1}{2}}^{1} \frac{2x^2+x}{x^2+x}dx=\left[ xln(x^2+x)\right]_{\frac{1}{2}}^{1}-\int_{\frac{1}{2}}^{1} \frac{2x^2+2x-x}{x^2+x}dx=\left[ xln(x^2+x)-2x\right]_{\frac{1}{2}}^{1}+\int_{\frac{1}{2}}^{1} \frac{x}{x^2+x}dx=} \displaystyle{=\left[ xln(x^2+x)\right]_{\frac{1}{2}}^{1}-\int_{\frac{1}{2}}^{1} \frac{2x^2+x}{x^2+x}dx=\left[ xln(x^2+x)\right]_{\frac{1}{2}}^{1}-\int_{\frac{1}{2}}^{1} \frac{2x^2+2x-x}{x^2+x}dx=\left[ xln(x^2+x)-2x\right]_{\frac{1}{2}}^{1}+\int_{\frac{1}{2}}^{1} \frac{x}{x^2+x}dx=}](/forum/ext/geomar/texintegr/latexrender/pictures/6610356a44ab53aa87721b8134b2eef6.png)
![\displaystyle{=\left[ xln(x^2+x)-2x\right]_{\frac{1}{2}}^{1}+\int_{\frac{1}{2}}^{1} \frac{x}{x^2+x}dx=\left[ xln(x^2+x)-2x\right]_{\frac{1}{2}}^{1}+\int_{\frac{1}{2}}^{1} \frac{1}{x+1}dx=\left[ xln(x^2+x)-2x+ln|x+1|\right]_{\frac{1}{2}}^{1}=} \displaystyle{=\left[ xln(x^2+x)-2x\right]_{\frac{1}{2}}^{1}+\int_{\frac{1}{2}}^{1} \frac{x}{x^2+x}dx=\left[ xln(x^2+x)-2x\right]_{\frac{1}{2}}^{1}+\int_{\frac{1}{2}}^{1} \frac{1}{x+1}dx=\left[ xln(x^2+x)-2x+ln|x+1|\right]_{\frac{1}{2}}^{1}=}](/forum/ext/geomar/texintegr/latexrender/pictures/86ad6114f509001ee742791d8315ffb9.png)
![\displaystyle{= 1 \cdot ln(1^2+1)-2 \cdot1+ln|1+1|\right- \frac{1}{2}ln\left(\frac{1}{4}+\frac{1}{2} \right)-2\frac{1}{2}+ln\left|\frac{1}{2}+1 \right|\right]=} \displaystyle{= 1 \cdot ln(1^2+1)-2 \cdot1+ln|1+1|\right- \frac{1}{2}ln\left(\frac{1}{4}+\frac{1}{2} \right)-2\frac{1}{2}+ln\left|\frac{1}{2}+1 \right|\right]=}](/forum/ext/geomar/texintegr/latexrender/pictures/ccbcf2b15612b98ace3a85b5bd67a5b9.png)
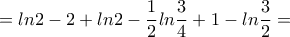

 .
.