exdx έγραψε: ↑Τετ Μάιος 23, 2018 7:57 am
Δίνεται η συνάρτηση
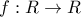
με

.
α) Να τη μελετήσετε ως προς τη μονοτονία και την κυρτότητα .
β) Να βρείτε τις ασύμπτωτες και να σχεδιάσετε τη γραφική παράσταση .
γ) Να υπολογίσετε το

.
δ) Αν

να δείξετε ότι η ευθεία

τέμνει τη

σε τρία ακριβώς σημεία .
Η ιδέα είναι από εφαρμογή του σχολικού. Χωρίς λύση στο δ.
α) Η

είναι παραγωγίσιμη στο

με παράγωγο

άρα είναι γνησίως αύξουσα στο
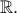

Η

είναι λοιπόν κοίλη στο
![\displaystyle ( - \infty ,0] \displaystyle ( - \infty ,0]](/forum/ext/geomar/texintegr/latexrender/pictures/c6f1873ce598613d4230a28ea6af36e7.png)
και κυρτή στο

β) Η

είναι συνεχής στο
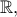
οπότε δεν έχει κατακόρυφες ασύμπτωτες.
![\displaystyle \mathop {\lim }\limits_{x \to - \infty } [f(x) - (x + 2)] = - \mathop {\lim }\limits_{x \to - \infty } \frac{{4{e^x}}}{{{e^x} + 1}} = 0 \displaystyle \mathop {\lim }\limits_{x \to - \infty } [f(x) - (x + 2)] = - \mathop {\lim }\limits_{x \to - \infty } \frac{{4{e^x}}}{{{e^x} + 1}} = 0](/forum/ext/geomar/texintegr/latexrender/pictures/61dd4ba2bddf91f8e4b6912735b2a7e4.png)
και η ευθεία

είναι πλάγια ασύμπτωτη στο


- Με απλά υλικά (9).png (7.9 KiB) Προβλήθηκε 1373 φορές
Εξάλλου, η

είναι περιττή. Πράγματι, για κάθε

είναι:

Άρα,
![\displaystyle f(x) = x - 2 + \frac{4}{{{e^x} + 1}} \Rightarrow \mathop {\lim }\limits_{x \to + \infty } [f(x) - (x - 2)] = \mathop {\lim }\limits_{x \to + \infty } \frac{4}{{{e^x} + 1}} = 0, \displaystyle f(x) = x - 2 + \frac{4}{{{e^x} + 1}} \Rightarrow \mathop {\lim }\limits_{x \to + \infty } [f(x) - (x - 2)] = \mathop {\lim }\limits_{x \to + \infty } \frac{4}{{{e^x} + 1}} = 0,](/forum/ext/geomar/texintegr/latexrender/pictures/f5fc43485107dbabf34febc988ede944.png)
δηλαδή η ευθεία

είναι πλάγια ασύμπτωτη στο
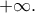
γ) Επειδή η

είναι περιττή,

(η απόδειξη είναι κλασική).
δ) Μία απόπειρα με κάθε επιφύλαξη. Δεν ξέρω κατά πόσο στέκει.
Για

η ευθεία

τέμνει την ασύμπτωτη

στο σημείο με τετμημένη

Αν

οπότε η

τέμνει την

σε κάποιο σημείο στο

Η

όμως σε αυτό
το διάστημα είναι κοίλη και βρίσκεται κάτω από την ασύμπτωτή της στο

, οπότε η

θα τέμνει υποχρεωτικά την

σε ένα σημείο με τετμημένη στο

Ομοίως εργαζόμαστε και με την ασύμπτωτη

Τέλος έχουμε και το προφανές κοινό σημείο που είναι η αρχή των αξόνων, δηλαδή ακριβώς τρία κοινά σημεία.
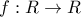 με
με  .
. .
.  να δείξετε ότι η ευθεία
να δείξετε ότι η ευθεία  τέμνει τη
τέμνει τη  σε τρία ακριβώς σημεία .
σε τρία ακριβώς σημεία .
 είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  με παράγωγο
με παράγωγο  άρα είναι γνησίως αύξουσα στο
άρα είναι γνησίως αύξουσα στο 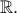
 Η
Η ![\displaystyle ( - \infty ,0] \displaystyle ( - \infty ,0]](/forum/ext/geomar/texintegr/latexrender/pictures/c6f1873ce598613d4230a28ea6af36e7.png) και κυρτή στο
και κυρτή στο 
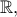 οπότε δεν έχει κατακόρυφες ασύμπτωτες.
οπότε δεν έχει κατακόρυφες ασύμπτωτες.![\displaystyle \mathop {\lim }\limits_{x \to - \infty } [f(x) - (x + 2)] = - \mathop {\lim }\limits_{x \to - \infty } \frac{{4{e^x}}}{{{e^x} + 1}} = 0 \displaystyle \mathop {\lim }\limits_{x \to - \infty } [f(x) - (x + 2)] = - \mathop {\lim }\limits_{x \to - \infty } \frac{{4{e^x}}}{{{e^x} + 1}} = 0](/forum/ext/geomar/texintegr/latexrender/pictures/61dd4ba2bddf91f8e4b6912735b2a7e4.png) και η ευθεία
και η ευθεία  είναι πλάγια ασύμπτωτη στο
είναι πλάγια ασύμπτωτη στο 
 είναι:
είναι: 
![\displaystyle f(x) = x - 2 + \frac{4}{{{e^x} + 1}} \Rightarrow \mathop {\lim }\limits_{x \to + \infty } [f(x) - (x - 2)] = \mathop {\lim }\limits_{x \to + \infty } \frac{4}{{{e^x} + 1}} = 0, \displaystyle f(x) = x - 2 + \frac{4}{{{e^x} + 1}} \Rightarrow \mathop {\lim }\limits_{x \to + \infty } [f(x) - (x - 2)] = \mathop {\lim }\limits_{x \to + \infty } \frac{4}{{{e^x} + 1}} = 0,](/forum/ext/geomar/texintegr/latexrender/pictures/f5fc43485107dbabf34febc988ede944.png) δηλαδή η ευθεία
δηλαδή η ευθεία είναι πλάγια ασύμπτωτη στο
είναι πλάγια ασύμπτωτη στο 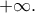
 (η απόδειξη είναι κλασική).
(η απόδειξη είναι κλασική). τέμνει την ασύμπτωτη
τέμνει την ασύμπτωτη  στο σημείο με τετμημένη
στο σημείο με τετμημένη 
 οπότε η
οπότε η  Η
Η  , οπότε η
, οπότε η 


 και αφού είναι περιττή αρκεί να αποδείξουμε
και αφού είναι περιττή αρκεί να αποδείξουμε γιατί τότε θα έχει ακριβώς μια ρίζα
γιατί τότε θα έχει ακριβώς μια ρίζα 
 στο
στο  (Rolle)
(Rolle)
 με
με 

 με
με 
![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) μας δίνει αυτό που θέλουμε.
μας δίνει αυτό που θέλουμε. (στην περίπτωση μας είναι κυρτή) και να δείξουμε ότι η ευθεία
(στην περίπτωση μας είναι κυρτή) και να δείξουμε ότι η ευθεία  για συγκεκριμένες τιμές της παραμέτρου
για συγκεκριμένες τιμές της παραμέτρου  (εδώ κολλάω) τέμνει την γραφική παράστση της
(εδώ κολλάω) τέμνει την γραφική παράστση της  .
.  , αλλά δυσκολεύομαι να το διατυπώσω.
, αλλά δυσκολεύομαι να το διατυπώσω.
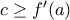 τότε εύκολα βλέπουμε ότι δεν υπάρχει ρίζα.
τότε εύκολα βλέπουμε ότι δεν υπάρχει ρίζα.
 είναι κυρτή το
είναι κυρτή το  υπάρχει στο
υπάρχει στο 
 .
. η
η  τότε υπάρχει ρίζα .
τότε υπάρχει ρίζα . κοντα στο
κοντα στο  με
με  και ο Bolzano μας την δίνει.
και ο Bolzano μας την δίνει.