Σελίδα 1 από 1
Εύρεση του τύπου συνάρτησης
Δημοσιεύτηκε: Σάβ Ιαν 08, 2011 5:37 pm
από KDORTSI
Re: Εύρεση του τύπου συνάρτησης
Δημοσιεύτηκε: Κυρ Ιαν 09, 2011 12:51 pm
από hsiodos
Καλημέρα
Έχουμε:

και

Από την (1) θέτοντας όπου x το 2x +1 παίρνουμε:
![\displaystyle{
a(2x + 1) < f(2x + 1) \le a(2x + 1) + 1 \Rightarrow ax(2x + 1) < xf(2x + 1) \le x\left[ {a(2x + 1) + 1} \right]} \displaystyle{
a(2x + 1) < f(2x + 1) \le a(2x + 1) + 1 \Rightarrow ax(2x + 1) < xf(2x + 1) \le x\left[ {a(2x + 1) + 1} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/087ae23b61a57b7fe9671c84577c94b0.png)
![\displaystyle{
\Rightarrow ax(2x + 1) + x + 1 < xf(2x + 1) + x + 1 \le x\left[ {a(2x + 1) + 1} \right] + x + 1} \displaystyle{
\Rightarrow ax(2x + 1) + x + 1 < xf(2x + 1) + x + 1 \le x\left[ {a(2x + 1) + 1} \right] + x + 1}](/forum/ext/geomar/texintegr/latexrender/pictures/51f5df8ef65f5026eef76f991706e73e.png)

Αν α < 0 τότε
![\displaystyle{\mathop {\lim }\limits_{x \to + \infty } \left[ {2ax^2 + (a +2)x + 1} \right] = - \infty } \displaystyle{\mathop {\lim }\limits_{x \to + \infty } \left[ {2ax^2 + (a +2)x + 1} \right] = - \infty }](/forum/ext/geomar/texintegr/latexrender/pictures/c43ded75d3d259b2163d88aae3222759.png)
οπότε θα υπάρχει

και έτσι από το δεύτερο σκέλος της (3) προκύπτει

που είναι άτοπο.
Συνεπώς α > 0
Από την (1) τώρα υψώνοντας στο τετράγωνο παίρνουμε ισοδύναμα:

Ο συνδυασμός των (3) και (4) μας δίνει ότι:

και


Αν α > 2 η (5) δεν μπορεί να ισχύει για κάθε x > 0 αφού το τριώνυμο έχει αρνητικό συντελεστή στο

(θετική διακρίνουσα) και ετερόσημες ρίζες.
Αν α < 2 η (6) προφανώς δεν ισχύει για κάθε x > 0 .
Προκύπτει ότι α = 2 και έτσι τα δεδομένα μας είναι:


Από την (1) προκύπτει ότι

όπου για τον αριθμό

(εξαρτώμενο από το x) ισχύει

Έστω τώρα ένας θετικός αριθμός x , θα είναι
 Εδώ υπάρχει λάθος αφού το σωστό είναι
Εδώ υπάρχει λάθος αφού το σωστό είναι  και μάλλον αυτό εννοεί (;) ο Νίκος στο μήνυμα του (πιο κάτω) . Άρα η λύση που ακολουθεί είναι άκυρη .
και μάλλον αυτό εννοεί (;) ο Νίκος στο μήνυμα του (πιο κάτω) . Άρα η λύση που ακολουθεί είναι άκυρη .



Αν

η τελευταία ισότητα μας οδηγεί σε άτοπο αφού το πρώτο μέλος είναι αρνητικός ενώ το δεύτερο θετικός αριθμός.
Άρα

για το τυχαίο x > 0 και έτσι

Γιώργος
Re: Εύρεση του τύπου συνάρτησης
Δημοσιεύτηκε: Κυρ Ιαν 09, 2011 2:00 pm
από mathxl
Μια απόδειξη για το α
Είναι

Για χ βάζουμε το 2χ+1 και λαμβάνουμε



διότι το α δεν είναι 0
Re: Εύρεση του τύπου συνάρτησης
Δημοσιεύτηκε: Κυρ Ιαν 09, 2011 3:47 pm
από Mihalis_Lambrou
mathxl έγραψε:Μια απόδειξη για το α
Λίγο αλλιώς: Από την

, έχουμε (όπως πριν)

.
Από την συναρτησιακή σχέση, διαιρώντας με το

έχουμε

.
Παίρνοντας όριο του

τείνοντος στο άπειρο λαμβάνουμε

, οπότε
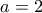
.
Φιλικά,
Μιχάλης
Re: Εύρεση του τύπου συνάρτησης
Δημοσιεύτηκε: Κυρ Ιαν 09, 2011 3:50 pm
από nikoszan
Στη λυση που προτεινει ο Γιωργος υπαρχει προς το τελος ενα λαθος
Φιλικα Ν.Ζανταριης
Re: Εύρεση του τύπου συνάρτησης
Δημοσιεύτηκε: Κυρ Ιαν 09, 2011 6:24 pm
από Mihalis_Lambrou
hsiodos έγραψε:
Έστω τώρα ένας θετικός αριθμός x , θα είναι

Συνεχίζω από εκεί που σταμάτησε ο Γιώργος αλλά δείχνω κάτι λιγότερο: Όχι ότι

αλλά ότι

. (Θα επανέλθω αν βρω χρόνο).
Η συναρτησιακή σχέση δίνει

ή

ή

Παίροντας όριο του

τείνοντος στο άπειρο βλεπουμε ότι το δεξί μέλος τείνει στο 3, συνεπώς

. Oπότε για

υπάρχει

που από κεί και πέρα είναι

δηλαδή

. Άρα και (εφόσον

)


. . . . .
προσθέτοντας κατά μέλη (η γεωμετρική πρόοδος είναι απλή) θα βρούμε

και επειδή αυτό ισχύει για κάθε ε >0, έπεται

. (Προσοχή, δεν μπορούμε να πούμε ότι

γιατί το

μας εξαρτάται από το ε.)
Φιλικά,
Μιχάλης
Υ.Γ. Θα χαρώ να συνεχίσει κάποιος από εδώ. Θα το κοιτάξω αργότερα. Τώρα ... πνίγομαι).
Re: Εύρεση του τύπου συνάρτησης
Δημοσιεύτηκε: Κυρ Ιαν 09, 2011 11:55 pm
από hsiodos
Mihalis_Lambrou έγραψε:hsiodos έγραψε:
Έστω τώρα ένας θετικός αριθμός x , θα είναι

Συνεχίζω από εκεί που σταμάτησε ο Γιώργος αλλά δείχνω κάτι λιγότερο: Όχι ότι

αλλά ότι

. (Θα επανέλθω αν βρω χρόνο).
.
Μιχάλη έχω αποδείξει και ότι

αλλά το ζητούμενο δεν μου προκύπτει !!!
Γιώργος
Re: Εύρεση του τύπου συνάρτησης
Δημοσιεύτηκε: Δευ Ιαν 10, 2011 10:32 pm
από Μάκης Χατζόπουλος
Προτεινόμενη λύση από τον
Νίκο Ζανταρίδη
Έχουμε,

και

Από την (1) έχουμε ότι για κάθε χ>0 ισχύει:

Είναι,

οπότε λόγω της (3) προκύπτει ότι:

Από την (2) έχουμε ότι για κάθε χ > 0 ισχύει:

ή

οπότε,
![\displaystyle{\mathop {\lim }\limits_{x \to + \infty } {\left( {\frac{{f\left( x \right)}}{x}} \right)^2} = \mathop {\lim }\limits_{x \to + \infty } \left[ {\left( {2 + \frac{1}{x}} \right) \cdot \frac{{f\left( {2x + 1} \right)}}{{2x + 1}} + \frac{1}{x} + \frac{1}{{{x^2}}}} \right]} \displaystyle{\mathop {\lim }\limits_{x \to + \infty } {\left( {\frac{{f\left( x \right)}}{x}} \right)^2} = \mathop {\lim }\limits_{x \to + \infty } \left[ {\left( {2 + \frac{1}{x}} \right) \cdot \frac{{f\left( {2x + 1} \right)}}{{2x + 1}} + \frac{1}{x} + \frac{1}{{{x^2}}}} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/c840c14a88c3179241f0b81f0d140d33.png)
άρα,

και επειδή το

βρίσκουμε

Άρα για κάθε χ > 0 ισχύει:

Θεωρώ την συνάρτηση:

Λόγω της (3) έχουμε:

(5)
Επίσης,

(αφού

και

)
και

Έτσι έχουμε,

για κάθε χ > 0
Επομένως, για κάθε χ > 0 ισχύει:

και επειδή

έχουμε:


(αφού

για κάθε χ > 0)
Άρα για κάθε

και για κάθε χ > 0 ισχύει:

οπότε,

δηλ.

δηλ.

επομένως

άρα

για κάθε χ > 0
 ισχύει:
ισχύει: , για καθε
, για καθε 
 και
και  , για καθε
, για καθε 
 ,για καθε
,για καθε  "
" ισχύει:
ισχύει: , για καθε
, για καθε 
 και
και  , για καθε
, για καθε 
 ,για καθε
,για καθε  "
" και
και 
![\displaystyle{
a(2x + 1) < f(2x + 1) \le a(2x + 1) + 1 \Rightarrow ax(2x + 1) < xf(2x + 1) \le x\left[ {a(2x + 1) + 1} \right]} \displaystyle{
a(2x + 1) < f(2x + 1) \le a(2x + 1) + 1 \Rightarrow ax(2x + 1) < xf(2x + 1) \le x\left[ {a(2x + 1) + 1} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/087ae23b61a57b7fe9671c84577c94b0.png)
![\displaystyle{
\Rightarrow ax(2x + 1) + x + 1 < xf(2x + 1) + x + 1 \le x\left[ {a(2x + 1) + 1} \right] + x + 1} \displaystyle{
\Rightarrow ax(2x + 1) + x + 1 < xf(2x + 1) + x + 1 \le x\left[ {a(2x + 1) + 1} \right] + x + 1}](/forum/ext/geomar/texintegr/latexrender/pictures/51f5df8ef65f5026eef76f991706e73e.png)

![\displaystyle{\mathop {\lim }\limits_{x \to + \infty } \left[ {2ax^2 + (a +2)x + 1} \right] = - \infty } \displaystyle{\mathop {\lim }\limits_{x \to + \infty } \left[ {2ax^2 + (a +2)x + 1} \right] = - \infty }](/forum/ext/geomar/texintegr/latexrender/pictures/c43ded75d3d259b2163d88aae3222759.png) οπότε θα υπάρχει
οπότε θα υπάρχει  και έτσι από το δεύτερο σκέλος της (3) προκύπτει
και έτσι από το δεύτερο σκέλος της (3) προκύπτει  που είναι άτοπο.
που είναι άτοπο.



 (θετική διακρίνουσα) και ετερόσημες ρίζες.
(θετική διακρίνουσα) και ετερόσημες ρίζες.
 όπου για τον αριθμό
όπου για τον αριθμό  (εξαρτώμενο από το x) ισχύει
(εξαρτώμενο από το x) ισχύει 





 η τελευταία ισότητα μας οδηγεί σε άτοπο αφού το πρώτο μέλος είναι αρνητικός ενώ το δεύτερο θετικός αριθμός.
η τελευταία ισότητα μας οδηγεί σε άτοπο αφού το πρώτο μέλος είναι αρνητικός ενώ το δεύτερο θετικός αριθμός. για το τυχαίο x > 0 και έτσι
για το τυχαίο x > 0 και έτσι 




 , έχουμε (όπως πριν)
, έχουμε (όπως πριν)  .
.  έχουμε
έχουμε .
. τείνοντος στο άπειρο λαμβάνουμε
τείνοντος στο άπειρο λαμβάνουμε , οπότε
, οπότε 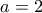 .
.
 αλλά ότι
αλλά ότι  . (Θα επανέλθω αν βρω χρόνο).
. (Θα επανέλθω αν βρω χρόνο). ή
ή ή
ή
 . Oπότε για
. Oπότε για  υπάρχει
υπάρχει  που από κεί και πέρα είναι
που από κεί και πέρα είναι  δηλαδή
δηλαδή . Άρα και (εφόσον
. Άρα και (εφόσον  )
)


 . (Προσοχή, δεν μπορούμε να πούμε ότι
. (Προσοχή, δεν μπορούμε να πούμε ότι  αλλά το ζητούμενο δεν μου προκύπτει !!!
αλλά το ζητούμενο δεν μου προκύπτει !!! και
και 



 ή
ή 
![\displaystyle{\mathop {\lim }\limits_{x \to + \infty } {\left( {\frac{{f\left( x \right)}}{x}} \right)^2} = \mathop {\lim }\limits_{x \to + \infty } \left[ {\left( {2 + \frac{1}{x}} \right) \cdot \frac{{f\left( {2x + 1} \right)}}{{2x + 1}} + \frac{1}{x} + \frac{1}{{{x^2}}}} \right]} \displaystyle{\mathop {\lim }\limits_{x \to + \infty } {\left( {\frac{{f\left( x \right)}}{x}} \right)^2} = \mathop {\lim }\limits_{x \to + \infty } \left[ {\left( {2 + \frac{1}{x}} \right) \cdot \frac{{f\left( {2x + 1} \right)}}{{2x + 1}} + \frac{1}{x} + \frac{1}{{{x^2}}}} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/c840c14a88c3179241f0b81f0d140d33.png)
 και επειδή το
και επειδή το  βρίσκουμε
βρίσκουμε 


 (5)
(5)
 και
και  )
)
 για κάθε χ > 0
για κάθε χ > 0


 και για κάθε χ > 0 ισχύει:
και για κάθε χ > 0 ισχύει: 

 δηλ.
δηλ.  άρα
άρα  για κάθε χ > 0
για κάθε χ > 0