![f,g:[0,1]\to (0,\infty) f,g:[0,1]\to (0,\infty)](/forum/ext/geomar/texintegr/latexrender/pictures/2a3ef1b0da13f3558a37b9770d9ebeb8.png) συνεχείς συναρτήσεις με
συνεχείς συναρτήσεις με  . Τότε, υπάρχει υποδιάστημα
. Τότε, υπάρχει υποδιάστημα ![[a,b]\subset [0,1] [a,b]\subset [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/46f651a104a9b701d721d819f9a76e3a.png) ώστε:
ώστε:  .
.Συντονιστής: Μπάμπης Στεργίου
![\displaystyle{F\left( \varepsilon \right) = \int\limits_\varepsilon ^{1 - \varepsilon } {f\left( t \right)dt} ,\varepsilon \in \left[ {0,\frac{1}{2}} \right]} \displaystyle{F\left( \varepsilon \right) = \int\limits_\varepsilon ^{1 - \varepsilon } {f\left( t \right)dt} ,\varepsilon \in \left[ {0,\frac{1}{2}} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/50f70f7dd0cb61d81295eee3368d9a12.png) , η οποία είναι συνεχής στο
, η οποία είναι συνεχής στο ![\displaystyle{\left[ {0,\frac{1}{2}} \right]} \displaystyle{\left[ {0,\frac{1}{2}} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/062e75b285e3a68e7d1a729836f19cee.png) και επίσης
και επίσης 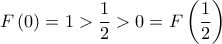 άρα από το θεώρημα ενδιάμεσης τιμής, θα υπάρχει τουλάχιστον ένα
άρα από το θεώρημα ενδιάμεσης τιμής, θα υπάρχει τουλάχιστον ένα  τέτοιο ώστε
τέτοιο ώστε  , δηλαδή υπάρχει διάστημα
, δηλαδή υπάρχει διάστημα ![\displaystyle{\left[ {{\varepsilon _0}.1 - {\varepsilon _0}} \right] \subset \left[ {0,1} \right]} \displaystyle{\left[ {{\varepsilon _0}.1 - {\varepsilon _0}} \right] \subset \left[ {0,1} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/788890dcb31b558a563aab81906f0e59.png) με
με  ώστε
ώστε  ,
,  . Ομοίως για την
. Ομοίως για την 
![\displaystyle{F\left( \varepsilon \right) = \int\limits_{\frac{1}{2} - \varepsilon }^{\frac{1}{2} + \varepsilon } {f\left( t \right)dt} ,\varepsilon \in \left[ {0,\frac{1}{2}} \right]} \displaystyle{F\left( \varepsilon \right) = \int\limits_{\frac{1}{2} - \varepsilon }^{\frac{1}{2} + \varepsilon } {f\left( t \right)dt} ,\varepsilon \in \left[ {0,\frac{1}{2}} \right]}](/forum/ext/geomar/texintegr/latexrender/pictures/0d4d19fe7f0a41d4fe69857f67716b0d.png)
Επαναφορά.
Νομίζω η ακόλουθη είναι εντός σχολικής ύλης.ΠΑΠΑΔΟΠΟΥΛΟΣ ΣΤΑΥΡΟΣ έγραψε: ↑Παρ Φεβ 01, 2019 11:06 amΕπαναφορά.
Νομίζω ότι δεν είναι κατάλληλος ο φάκελος
αν και η λύση που έχω είναι με σχολική ύλη .
 με
με  και άρα
και άρα 
 υπάρχει (μοναδικό)
υπάρχει (μοναδικό)  με
με  (η μοναδικότητα έπεται από το γεγονός ότι η
(η μοναδικότητα έπεται από το γεγονός ότι η  είναι γνήσια θετική και άρα το ολοκλήρωμα αυξάνει με το άνω άκρο του). Υπόψη ότι η
είναι γνήσια θετική και άρα το ολοκλήρωμα αυξάνει με το άνω άκρο του). Υπόψη ότι η  δίνει
δίνει  .
. είναι συνεχής καθώς ισχύει (απλό)
είναι συνεχής καθώς ισχύει (απλό)  (βγαίνει από τις ισότητες
(βγαίνει από τις ισότητες  )
) ορίζουμε μία αντίστοιχη
ορίζουμε μία αντίστοιχη 
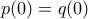 , τελειώσαμε. Χωρίς βλάβη, λοιπόν,
, τελειώσαμε. Χωρίς βλάβη, λοιπόν,  . Άρα
. Άρα  , οπότε
, οπότε  , από όπου
, από όπου  που μαζί με την
που μαζί με την  δίνει ότι
δίνει ότι με
με  .
.  και τελειώσαμε.
και τελειώσαμε.![f,g:[0,1]\to (0,\infty) f,g:[0,1]\to (0,\infty)](/forum/ext/geomar/texintegr/latexrender/pictures/2a3ef1b0da13f3558a37b9770d9ebeb8.png) συνεχείς συναρτήσεις με
συνεχείς συναρτήσεις με  φθίνουσα και
φθίνουσα και  αύξουσα (ή αντίστροφα) και
αύξουσα (ή αντίστροφα) και  . Τότε, για κάθε
. Τότε, για κάθε  υπάρχει υποδιάστημα
υπάρχει υποδιάστημα ![[a,b]\subset [0,1] [a,b]\subset [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/46f651a104a9b701d721d819f9a76e3a.png) ώστε:
ώστε:  .
. τέτοιο ώστε
τέτοιο ώστε 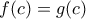 ,
,  για
για  ,
,  για
για 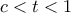 . Η δοθείσα συνθήκη
. Η δοθείσα συνθήκη 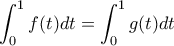 , ισοδύναμη προς την
, ισοδύναμη προς την  , μαζί με τις δοθείσες μονοτονίες και συνέχειες, συνεπάγεται ότι για κάθε
, μαζί με τις δοθείσες μονοτονίες και συνέχειες, συνεπάγεται ότι για κάθε  υπάρχει καλώς ορισμένο
υπάρχει καλώς ορισμένο  τέτοιο ώστε
τέτοιο ώστε 
 , παρατηρούμε ότι
, παρατηρούμε ότι  ,
,  (λόγω των
(λόγω των  ,
,  ). Λόγω συνέχειας υπάρχει
). Λόγω συνέχειας υπάρχει  τέτοιο ώστε
τέτοιο ώστε  . Η ζητούμενη γενίκευση προκύπτει για
. Η ζητούμενη γενίκευση προκύπτει για  .
. ,
,  , όπου τα
, όπου τα  ,
,  προκύπτουν από τις
προκύπτουν από τις  ,
,  .]
.]Για να παραλειφθούν ας μην γίνεται λόγος, καθώς ... όπως δείχνει το παρακάτω απλό παράδειγμα όπου οι δύο ισοεμβαδικές συναρτήσεις τέμνονται σε περισσότερα του ενός σημεία, δεν είναι δυνατόν να προκύψουν ίσα υποεμβαδά που να πλησιάζουν 'πολύ' το αρχικό εμβαδόν: αυτό γίνεται φανερό από την γεωμετρία και μόνον (αν κόψουμε 'πολύ' κοντά στα άκρα του διαστήματος, όπου η μία συνάρτηση υπερέχει της άλλης, δεν είναι δυνατόν να προκύψουν ίσα υποεμβαδά), αργότερα ελπίζω να στείλω και τις σχετικές εξισώσεις.
 ΔΕΝ έπεται η ύπαρξη υποδιαστήματος
ΔΕΝ έπεται η ύπαρξη υποδιαστήματος ![[a,b] [a,b]](/forum/ext/geomar/texintegr/latexrender/pictures/2c3d331bc98b44e71cb2aae9edadca7e.png) του
του ![[0,1] [0,1]](/forum/ext/geomar/texintegr/latexrender/pictures/ccfcd347d0bf65dc77afe01a3306a96b.png) τέτοιου ώστε
τέτοιου ώστε 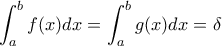 , όπου
, όπου  .
. και
και  ,
,  και
και  ,
,  και
και  ,
, 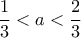 και
και  ,
, 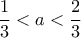 και
και  ,
,  και
και  , οι μόνες δύο που χρειάζεται να εξεταστούν είναι η πρώτη και η τελευταία: στην πρώτη (
, οι μόνες δύο που χρειάζεται να εξεταστούν είναι η πρώτη και η τελευταία: στην πρώτη (  και
και  ) η συνθήκη
) η συνθήκη  δίνει
δίνει 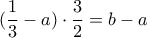 και
και  , οπότε
, οπότε  , στην τελευταία (
, στην τελευταία (  και
και  ) η συνθήκη
) η συνθήκη  δίνει
δίνει  και
και  (KAI
(KAI  λόγω
λόγω  ), οπότε
), οπότε  .]
.]Μέλη σε αυτήν τη Δ. Συζήτηση: Google [Bot] και 3 επισκέπτες