Σελίδα 1 από 1
Μιγαδικοί αριθμοί (επαναληπτικό)
Δημοσιεύτηκε: Δευ Ιούλ 08, 2013 12:33 pm
από thanasis kopadis
Δίνονται οι μιγαδικοί αριθμοί

για τους οποίους ισχύουν οι παρακάτω σχέσεις:

,
με 
και

α) Να αποδείξετε ότι η εικόνα του

στο μιγαδικό επίπεδο κινείται στον μοναδιαίο κύκλο.
β) Έστω οι μιγαδικοί

με

,

και
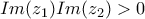
.
Δίνεται και η εξίσωση
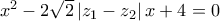
, με ρίζες τους

Να αποδείξετε ότι:
i) Οι

δεν είναι πραγματικοί αριθμοί και ότι

ii) Ισχύει:

γ) Να βρείτε την απόσταση των εικόνων

των μιγαδικών

και

αντίστοιχα, στο μιγαδικό επίπεδο.
(Δόθηκε επιπλέον δεδομένο, μετά από την παρατήρηση του συνάδελφου Μάγκου Θάνου)
Re: Μιγαδικοί αριθμοί (επαναληπτικό)
Δημοσιεύτηκε: Δευ Ιούλ 08, 2013 1:02 pm
από matha
thanasis kopadis έγραψε:Δίνονται οι μιγαδικοί αριθμοί

για τους οποίους ισχύουν οι παρακάτω σχέσεις:

και

α) Να αποδείξετε ότι η εικόνα του

στο μιγαδικό επίπεδο κινείται στον μοναδιαίο κύκλο.
Νομίζω υπάρχει πρόβλημα στο πρώτο ερώτημα, εκτός αν δε βλέπω εγώ κάτι.
Είναι

Επειδή το

είναι πραγματικός, θετικός, είναι

Ωστόσο, έχουμε πρόβλημα με το

Εκ των προτέρων δε γνωρίζουμε ότι ο εκθέτης

είναι θετικός ακέραιος, ώστε να εφαρμόσουμε την ιδιότητα

Re: Μιγαδικοί αριθμοί (επαναληπτικό)
Δημοσιεύτηκε: Δευ Ιούλ 08, 2013 1:11 pm
από thanasis kopadis
Έχεις δίκιο.Δεν το είχα σκεφτεί. Ίσως να μπορεί να βελτιωθεί με το επιπλέον δεδομένο

Ευχαριστώ πολύ για την παρατήρηση.
Re: Μιγαδικοί αριθμοί (επαναληπτικό)
Δημοσιεύτηκε: Δευ Ιούλ 08, 2013 3:19 pm
από dennys
1) Αφήνω στο 1 μέλος το

και μετράρω και θέτοντας

αρα τριώνυμο και απλά

2)οι σχέσεις που δίνονται σημαίνουν οτι οι

κινούνται στο ίδιο τεταρτημόριο και συνεπώς

το τριώνυμο έχει αρνητική διακρίνουσα , αρα

δεν είναι πραγματικοί.αρα είναι μιγαδικοί συζυγείς .
Ετσι

απο Vieta .
3) Ξεκινώντας απο το 1 μέλος με πράξεις

![(x_1-x_2)(\bar x_1-\bar x_2)+8|z_1-z_2|^{2}=...=4+4-[(x_1+x_2)^{2}-2x_1x_2]+8|z_1-z_2|^{2}= (x_1-x_2)(\bar x_1-\bar x_2)+8|z_1-z_2|^{2}=...=4+4-[(x_1+x_2)^{2}-2x_1x_2]+8|z_1-z_2|^{2}=](/forum/ext/geomar/texintegr/latexrender/pictures/9e4ea49361d254ecf49dd797ebef864e.png)

εύκολο απο Vieta
4)

Βουτσάς Διονυσης (dennys)
Re: Μιγαδικοί αριθμοί (επαναληπτικό)
Δημοσιεύτηκε: Δευ Ιούλ 08, 2013 4:57 pm
από thanasis kopadis
Ευχαριστώ Διονύση για την ενασχόληση.
Μια άλλη προσέγγιση για το ερώτημα β).
i) Θέτω
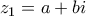
και

με
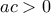
και

![D=8\left|z_1-z_2 \right|^2-16=8\left|a+bi-c-di \right|^2-16=8[(a-c)^2+(b-d)^2]-16=8(a^2+c^2-2ac+b^2+d^2-2bd)-16= D=8\left|z_1-z_2 \right|^2-16=8\left|a+bi-c-di \right|^2-16=8[(a-c)^2+(b-d)^2]-16=8(a^2+c^2-2ac+b^2+d^2-2bd)-16=](/forum/ext/geomar/texintegr/latexrender/pictures/19c5d3c65c8014efaef5688a9385cc48.png)
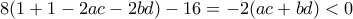
. Άρα το τριώνυμο έχει δύο ρίζες

που δεν είναι πραγματικές και άρα είναι συζυγείς μιγαδικοί.
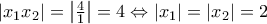
, αφού οι

έχουν ίσα μέτρα, ως συζυγείς.
ii) Eίναι

Οπότε
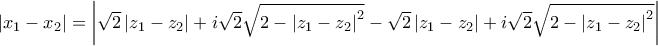
Δηλαδή

Υψώνοντας στο τετράγωνο προκύπτει:

, οπότε το ζητούμενο.
 για τους οποίους ισχύουν οι παρακάτω σχέσεις:
για τους οποίους ισχύουν οι παρακάτω σχέσεις: , με
, με  και
και 
 στο μιγαδικό επίπεδο κινείται στον μοναδιαίο κύκλο.
στο μιγαδικό επίπεδο κινείται στον μοναδιαίο κύκλο. με
με  ,
,  και
και 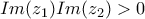 .
. 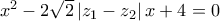 , με ρίζες τους
, με ρίζες τους 
 δεν είναι πραγματικοί αριθμοί και ότι
δεν είναι πραγματικοί αριθμοί και ότι 

 των μιγαδικών
των μιγαδικών  και
και  αντίστοιχα, στο μιγαδικό επίπεδο.
αντίστοιχα, στο μιγαδικό επίπεδο. για τους οποίους ισχύουν οι παρακάτω σχέσεις:
για τους οποίους ισχύουν οι παρακάτω σχέσεις: , με
, με  και
και 
 στο μιγαδικό επίπεδο κινείται στον μοναδιαίο κύκλο.
στο μιγαδικό επίπεδο κινείται στον μοναδιαίο κύκλο. με
με  ,
,  και
και 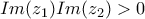 .
. 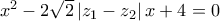 , με ρίζες τους
, με ρίζες τους 
 δεν είναι πραγματικοί αριθμοί και ότι
δεν είναι πραγματικοί αριθμοί και ότι 

 των μιγαδικών
των μιγαδικών  και
και  αντίστοιχα, στο μιγαδικό επίπεδο.
αντίστοιχα, στο μιγαδικό επίπεδο.
 είναι πραγματικός, θετικός, είναι
είναι πραγματικός, θετικός, είναι 

 είναι θετικός ακέραιος, ώστε να εφαρμόσουμε την ιδιότητα
είναι θετικός ακέραιος, ώστε να εφαρμόσουμε την ιδιότητα 
 και μετράρω και θέτοντας
και μετράρω και θέτοντας 

 το τριώνυμο έχει αρνητική διακρίνουσα , αρα
το τριώνυμο έχει αρνητική διακρίνουσα , αρα  απο Vieta .
απο Vieta .
![(x_1-x_2)(\bar x_1-\bar x_2)+8|z_1-z_2|^{2}=...=4+4-[(x_1+x_2)^{2}-2x_1x_2]+8|z_1-z_2|^{2}= (x_1-x_2)(\bar x_1-\bar x_2)+8|z_1-z_2|^{2}=...=4+4-[(x_1+x_2)^{2}-2x_1x_2]+8|z_1-z_2|^{2}=](/forum/ext/geomar/texintegr/latexrender/pictures/9e4ea49361d254ecf49dd797ebef864e.png)
 εύκολο απο Vieta
εύκολο απο Vieta
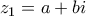 και
και  με
με 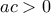 και
και 
![D=8\left|z_1-z_2 \right|^2-16=8\left|a+bi-c-di \right|^2-16=8[(a-c)^2+(b-d)^2]-16=8(a^2+c^2-2ac+b^2+d^2-2bd)-16= D=8\left|z_1-z_2 \right|^2-16=8\left|a+bi-c-di \right|^2-16=8[(a-c)^2+(b-d)^2]-16=8(a^2+c^2-2ac+b^2+d^2-2bd)-16=](/forum/ext/geomar/texintegr/latexrender/pictures/19c5d3c65c8014efaef5688a9385cc48.png)
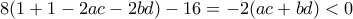 . Άρα το τριώνυμο έχει δύο ρίζες
. Άρα το τριώνυμο έχει δύο ρίζες 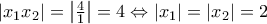 , αφού οι
, αφού οι 
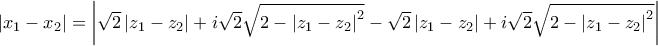

 , οπότε το ζητούμενο.
, οπότε το ζητούμενο.