 , δυο φορές παραγωγίσιμη με την ιδιότητα :
, δυο φορές παραγωγίσιμη με την ιδιότητα : υπάρχει
 ώστε για κάθε
ώστε για κάθε  με
με  να ισχύει :
να ισχύει :  .
.Να αποδείξετε ότι
 .
.Συντονιστής: Μπάμπης Στεργίου
Χωρίς βλάβη στην γενικότητα υπάρχουνexdx έγραψε:Έστω η συνάρτηση, δυο φορές παραγωγίσιμη με την ιδιότητα :
υπάρχειώστε για κάθε
με
να ισχύει :
.
Να αποδείξετε ότι.
 τέτοια ώστε
τέτοια ώστε  (για την ανάποδη ανισότητα εργαζόμαστε όμοια).
(για την ανάποδη ανισότητα εργαζόμαστε όμοια).  . Θα δείξω πρώτα ότι ισχύει
. Θα δείξω πρώτα ότι ισχύει  . Πράγματι, έστω
. Πράγματι, έστω  (η ισότητα αποκλείεται από την υπόθεση). Τότε από το Θ.Μ.Τ. στην
(η ισότητα αποκλείεται από την υπόθεση). Τότε από το Θ.Μ.Τ. στην  θα υπήρχε
θα υπήρχε  στο μεσοδιάστημα των
στο μεσοδιάστημα των  με
με  , που αντιβαίνει στην υπόθεση.
, που αντιβαίνει στην υπόθεση.  , ισχύει
, ισχύει  . Στη αντίθετη περίπτωση θα οδηγηθούμε σε άτοπο καθώς από το Θ.Μ.Τ. στην
. Στη αντίθετη περίπτωση θα οδηγηθούμε σε άτοπο καθώς από το Θ.Μ.Τ. στην  θα υπήρχε
θα υπήρχε  στο μεσοδιάστημα των
στο μεσοδιάστημα των  με
με  , που πάλι αντιβαίνει στην υπόθεση.
, που πάλι αντιβαίνει στην υπόθεση. τυχαίο. Διακρίνοντας περιπτώσεις όπου
τυχαίο. Διακρίνοντας περιπτώσεις όπου  ή
ή  (που εξαντλούν όλες τις εκδοχές αφού
(που εξαντλούν όλες τις εκδοχές αφού  ) και με παρόμοιο συλλογισμό μπορούμε εύκολα να δείξουμε ότι για οποιοδήποτε
) και με παρόμοιο συλλογισμό μπορούμε εύκολα να δείξουμε ότι για οποιοδήποτε  που ικανοποιεί
που ικανοποιεί  ή, αντίστοιχα,
ή, αντίστοιχα,  , ισχύει
, ισχύει  .
. στην τελευταία, έπεται
στην τελευταία, έπεται  . Αυτό σημαίνει ότι το
. Αυτό σημαίνει ότι το  είναι ολικό ελάχιστο της
είναι ολικό ελάχιστο της  . Συμπεραίνουμε ότι
. Συμπεραίνουμε ότι  , όπως θέλαμε.
, όπως θέλαμε.
 οπότε από την
οπότε από την  έχουμε ότι :
έχουμε ότι : άρα η
άρα η  είναι
είναι  και αφού είναι συνεχής θα είναι γνησίως μονότονη
και αφού είναι συνεχής θα είναι γνησίως μονότονη θα είναι γνησίως αύξουσα οπότε
θα είναι γνησίως αύξουσα οπότε  (το οποίο επίσης θέλει απόδειξη . Δείτε μια σχετική συζήτηση εδώ )
(το οποίο επίσης θέλει απόδειξη . Δείτε μια σχετική συζήτηση εδώ ) είναι γνησίως φθίνουσα τότε
είναι γνησίως φθίνουσα τότε 
 , για κάθε
, για κάθε 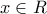
 , για κάθε
, για κάθε 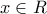
 έχει ακρότατο για
έχει ακρότατο για  οπότε από το θεώρημα Fermat προκύπτει ότι
οπότε από το θεώρημα Fermat προκύπτει ότι 
 παρουσιάζει σημείο καμπής για
παρουσιάζει σημείο καμπής για  ;
;
 παραγωγίσιμη στο
παραγωγίσιμη στο  και στο
και στο  ως πηλίκο παραγωγίσιμων και
ως πηλίκο παραγωγίσιμων και , και η ιδιότητα αποδείχτηκε.
, και η ιδιότητα αποδείχτηκε. ή
ή  για κάθε
για κάθε 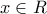 .
. είναι συνεχής ως διαφορά συνεχών και δεν μηδενίζεται ποτέ, άρα διατηρεί πρόσημο.
είναι συνεχής ως διαφορά συνεχών και δεν μηδενίζεται ποτέ, άρα διατηρεί πρόσημο. και
και  το θεώρημα Fermat εξασφαλίζει
το θεώρημα Fermat εξασφαλίζει  , όπως θέλαμε. Ομοίως και στην άλλη περίπτωση.
, όπως θέλαμε. Ομοίως και στην άλλη περίπτωση.Η πρώτη παρατήρηση είναι ότι δεν χρειάζεται η συνάρτηση να είναι δυο φορές παραγωγίσημη.Mihalis_Lambrou έγραψε: ↑Σάβ Αύγ 29, 2015 5:04 pmΧωρίς βλάβη στην γενικότητα υπάρχουνexdx έγραψε:Έστω η συνάρτηση, δυο φορές παραγωγίσιμη με την ιδιότητα :
υπάρχειώστε για κάθε
με
να ισχύει :
.
Να αποδείξετε ότι.
τέτοια ώστε
(για την ανάποδη ανισότητα εργαζόμαστε όμοια).
Έστω. Θα δείξω πρώτα ότι ισχύει
. Πράγματι, έστω
(η ισότητα αποκλείεται από την υπόθεση). Τότε από το Θ.Μ.Τ. στην
θα υπήρχε
στο μεσοδιάστημα των
με
, που αντιβαίνει στην υπόθεση.
Όμοια, αν, ισχύει
. Στη αντίθετη περίπτωση θα οδηγηθούμε σε άτοπο καθώς από το Θ.Μ.Τ. στην
θα υπήρχε
στο μεσοδιάστημα των
με
, που πάλι αντιβαίνει στην υπόθεση.
Έστω τώρατυχαίο. Διακρίνοντας περιπτώσεις όπου
ή
(που εξαντλούν όλες τις εκδοχές αφού
) και με παρόμοιο συλλογισμό μπορούμε εύκολα να δείξουμε ότι για οποιοδήποτε
που ικανοποιεί
ή, αντίστοιχα,
, ισχύει
.
Παίρνοντας όριοστην τελευταία, έπεται
. Αυτό σημαίνει ότι το
είναι ολικό ελάχιστο της
. Συμπεραίνουμε ότι
, όπως θέλαμε.
Φιλικά,
Μιχάλης
 .
. έχει ολικό ακρότατο στο
έχει ολικό ακρότατο στο  .
. είναι
είναι 
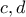 με
με

![\displaystyle g:[0,1]\rightarrow \mathbb{R} \displaystyle g:[0,1]\rightarrow \mathbb{R}](/forum/ext/geomar/texintegr/latexrender/pictures/5e9359ef56df31eafdd82110078112ec.png)


 με
με 
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης