erxmer έγραψε:Εστω οι συνεχείς συναρτήσεις

ώστε η

να είναι γνήσια αύξουσα και η

να είναι γνήσια φθίνουσα στο

. Aν

είναι αρχικές τους και υπάρχει

ώστε

και
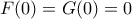
δείξτε οτι:
1) Η

είναι κυρτή και η

κοίλη
2) H συνάρτηση

είναι γνήσια αύξουσα
3)

Yγ ελπίζω μετα τις αλλαγές που προτείνατε να μην έχει κάτι άλλο...
...ΛΥΣΗ....
1) Επειδή

που είναι γνήσια αύξουσα, η

είναι κυρτή και επειδή
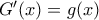
που είναι γνήσια φθίνουσα στο

, η

είναι κοίλη.
2) Είναι
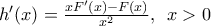
(1) και στο διάστημα
![[0,\,\,x],\,\,x>0 [0,\,\,x],\,\,x>0](/forum/ext/geomar/texintegr/latexrender/pictures/2f964a8aba4d81c312b43a554f1d960d.png)
σύμφωνα με το θεώρημα μέσης τιμής για την παραγωγίσιμη

, υπάρχει

ώστε

επομένως από (1)

γιατί

να είναι γνήσια αύξουσα και
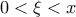
άρα η

είναι γνήσια αύξουσα στο

3) Θέλουμε

ή

Λόγω του (2) για

Τώρα για την

Είναι

(2) και στο διάστημα
![[0,\,\,x],\,\,x>0 [0,\,\,x],\,\,x>0](/forum/ext/geomar/texintegr/latexrender/pictures/2f964a8aba4d81c312b43a554f1d960d.png)
σύμφωνα με το θεώρημα μέσης τιμής για την παραγωγίσιμη

, υπάρχει

ώστε

επομένως από (1)

γιατί

είναι γνήσια φθίνουσα και
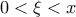
άρα η

είναι γνήσια φθίνουσα στο

Άρα για

επομένως ισχύει ότι

ή

Φιλικά και Μαθηματικά
Βασίλης
 ώστε η
ώστε η  να είναι γνήσια αύξουσα και η
να είναι γνήσια αύξουσα και η  να είναι γνήσια φθίνουσα στο
να είναι γνήσια φθίνουσα στο  . Aν
. Aν  είναι αρχικές τους και υπάρχει
είναι αρχικές τους και υπάρχει  ώστε
ώστε  και
και 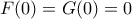 δείξτε οτι:
δείξτε οτι: είναι κυρτή και η
είναι κυρτή και η  κοίλη
κοίλη είναι γνήσια αύξουσα
είναι γνήσια αύξουσα

 ώστε
ώστε 





 η
η 

 που είναι γνήσια αύξουσα, η
που είναι γνήσια αύξουσα, η 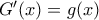 που είναι γνήσια φθίνουσα στο
που είναι γνήσια φθίνουσα στο 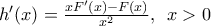 (1) και στο διάστημα
(1) και στο διάστημα ![[0,\,\,x],\,\,x>0 [0,\,\,x],\,\,x>0](/forum/ext/geomar/texintegr/latexrender/pictures/2f964a8aba4d81c312b43a554f1d960d.png) σύμφωνα με το θεώρημα μέσης τιμής για την παραγωγίσιμη
σύμφωνα με το θεώρημα μέσης τιμής για την παραγωγίσιμη  ώστε
ώστε  επομένως από (1)
επομένως από (1)  γιατί
γιατί 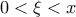 άρα η
άρα η 


 Είναι
Είναι  (2) και στο διάστημα
(2) και στο διάστημα 

 επομένως ισχύει ότι
επομένως ισχύει ότι  ή
ή 

 θα έχουμε
θα έχουμε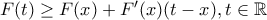
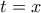

 παίρνουμε
παίρνουμε 
 είναι γνησίως φθίνουσα.
είναι γνησίως φθίνουσα. \displaystyle{-G
\displaystyle{-G \Rightarrow}
\Rightarrow} γνησίως
γνησίως  γνησίως φθίνουσα
γνησίως φθίνουσα