 με
με  ώστε
ώστε ![\displaystyle{[f'(x)]^2+f(x)f''(x)-f(x)f'(x)=1-x, x \in R} \displaystyle{[f'(x)]^2+f(x)f''(x)-f(x)f'(x)=1-x, x \in R}](/forum/ext/geomar/texintegr/latexrender/pictures/70d42e12986d7c47cb660069c679debb.png) .
.1) Nα βρεθεί ο τύπος της συνάρτησης
2)

3) Αν
 να βρεθεί η αντίστροφή της και να υπολογιστεί το
να βρεθεί η αντίστροφή της και να υπολογιστεί το 
4)
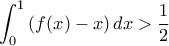
5)

6)

7) Nα λυθεί η εξίσωση

8)
![\displaystyle{\lim_{x \to +\infty}\frac{sin\left ( ln^3x \right )}{\sqrt[4]{x^2+1}}=0} \displaystyle{\lim_{x \to +\infty}\frac{sin\left ( ln^3x \right )}{\sqrt[4]{x^2+1}}=0}](/forum/ext/geomar/texintegr/latexrender/pictures/680486a7752282fd60fc940463ce5a55.png)
συνέχεια απο αυτή
Συντονιστής: Μπάμπης Στεργίου
 με
με  ώστε
ώστε ![\displaystyle{[f'(x)]^2+f(x)f''(x)-f(x)f'(x)=1-x, x \in R} \displaystyle{[f'(x)]^2+f(x)f''(x)-f(x)f'(x)=1-x, x \in R}](/forum/ext/geomar/texintegr/latexrender/pictures/70d42e12986d7c47cb660069c679debb.png) .
.
 να βρεθεί η αντίστροφή της και να υπολογιστεί το
να βρεθεί η αντίστροφή της και να υπολογιστεί το 
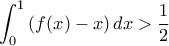



![\displaystyle{\lim_{x \to +\infty}\frac{sin\left ( ln^3x \right )}{\sqrt[4]{x^2+1}}=0} \displaystyle{\lim_{x \to +\infty}\frac{sin\left ( ln^3x \right )}{\sqrt[4]{x^2+1}}=0}](/forum/ext/geomar/texintegr/latexrender/pictures/680486a7752282fd60fc940463ce5a55.png)
![\displaystyle{\begin{array}{l}
{[f'(x)]^2} + f(x)f''(x) - f(x)f'(x) = 1 - x \Rightarrow {\left( {2f(x)f'(x)} \right)^\prime } - 2f(x)f'(x) = 2 - 2x \Rightarrow \\
\Rightarrow {\left( {{{\left( {{f^2}(x)} \right)}^\prime }} \right)^\prime } - {\left( {{f^2}(x)} \right)^\prime } = 2 - 2x \Rightarrow {\left( {{f^2}(x)} \right)^\prime } - {f^2}(x) = 2x - {x^2} + {c_1} \Rightarrow {\left( {{f^2}(x)} \right)^\prime } - {f^2}(x) = 2x - {x^2} - 1 \Rightarrow \\
\Rightarrow {\left( {{f^2}(x)} \right)^\prime }{e^{ - x}} + {\left( {{e^{ - x}}} \right)^\prime }{f^2}(x) = 2x{e^{ - x}} - {x^2}{e^{ - x}} - {e^{ - x}} \Rightarrow {\left( {{e^{ - x}}{f^2}(x)} \right)^\prime } = {\left( {{x^2}{e^{ - x}} + {e^{ - x}}} \right)^\prime } \Rightarrow \\
{e^{ - x}}{f^2}(x) = {x^2}{e^{ - x}} + {e^{ - x}} + c \\
\end{array}} \displaystyle{\begin{array}{l}
{[f'(x)]^2} + f(x)f''(x) - f(x)f'(x) = 1 - x \Rightarrow {\left( {2f(x)f'(x)} \right)^\prime } - 2f(x)f'(x) = 2 - 2x \Rightarrow \\
\Rightarrow {\left( {{{\left( {{f^2}(x)} \right)}^\prime }} \right)^\prime } - {\left( {{f^2}(x)} \right)^\prime } = 2 - 2x \Rightarrow {\left( {{f^2}(x)} \right)^\prime } - {f^2}(x) = 2x - {x^2} + {c_1} \Rightarrow {\left( {{f^2}(x)} \right)^\prime } - {f^2}(x) = 2x - {x^2} - 1 \Rightarrow \\
\Rightarrow {\left( {{f^2}(x)} \right)^\prime }{e^{ - x}} + {\left( {{e^{ - x}}} \right)^\prime }{f^2}(x) = 2x{e^{ - x}} - {x^2}{e^{ - x}} - {e^{ - x}} \Rightarrow {\left( {{e^{ - x}}{f^2}(x)} \right)^\prime } = {\left( {{x^2}{e^{ - x}} + {e^{ - x}}} \right)^\prime } \Rightarrow \\
{e^{ - x}}{f^2}(x) = {x^2}{e^{ - x}} + {e^{ - x}} + c \\
\end{array}}](/forum/ext/geomar/texintegr/latexrender/pictures/5a13922e5378edbbd11fff7fd7144c0b.png)
 άρα
άρα 
 και η
και η  συνεχής οπότε διατηρεί πρόσημο κι αφού
συνεχής οπότε διατηρεί πρόσημο κι αφού  θα είναι :
θα είναι :
Καλησπέρα στην εκλεκτή παρέα.erxmer έγραψε:Δίνεται συνάρτησημε
ώστε
.
1) Nα βρεθεί ο τύπος της συνάρτησης
2)
3) Αννα βρεθεί η αντίστροφή της και να υπολογιστεί το
4)
5)
6)
7) Nα λυθεί η εξίσωση
8)
συνέχεια απο αυτή
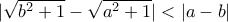

 (1)
(1) στο
στο ![[a,b]. [a,b].](/forum/ext/geomar/texintegr/latexrender/pictures/d5f1c430bf683ed676382edef55aa192.png)
 τέτοιο ώστε :
τέτοιο ώστε :  .
. 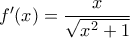 . Επομένως λόγω της (1) αρκεί να δείξω:
. Επομένως λόγω της (1) αρκεί να δείξω:



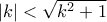



 , ισχύει.
, ισχύει. . Άρα η
. Άρα η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο  , συνεπώς και
, συνεπώς και 
 έχουμε :
έχουμε : 
 . Είναι
. Είναι  και έχουμε δεκτή ρίζα την θετική,
και έχουμε δεκτή ρίζα την θετική,  .
.

 .
.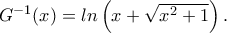
 .
.
![\displaystyle{f(x)-x=\sqrt{{{x}^{2}}+1}-x\ge 1-x\Rightarrow \int_{0}^{1}{(f(x)-x)dx>\int_{0}^{1}{(1-x)}}dx=\left[ x-\frac{{{x}^{2}}}{2} \right]_{0}^{1}=\frac{1}{2}} \displaystyle{f(x)-x=\sqrt{{{x}^{2}}+1}-x\ge 1-x\Rightarrow \int_{0}^{1}{(f(x)-x)dx>\int_{0}^{1}{(1-x)}}dx=\left[ x-\frac{{{x}^{2}}}{2} \right]_{0}^{1}=\frac{1}{2}}](/forum/ext/geomar/texintegr/latexrender/pictures/523afe903e7548a21cb9be8dd03c18f7.png)



 έχουμε ότι
έχουμε ότι ![\displaystyle{\underset{x\to +\infty }{\mathop{\lim }}\,\frac{sin\left( l{{n}^{3}}x \right)}{\sqrt[4]{{{x}^{2}}+1}}=\underset{x\to +\infty }{\mathop{\lim }}\,\frac{sin\left( l{{n}^{3}}x \right)}{\sqrt{x}}\frac{\sqrt{x}}{\sqrt{x}\sqrt[4]{1+\frac{1}{{{x}^{2}}}}}=\underset{x\to +\infty }{\mathop{\lim }}\,\frac{sin\left( l{{n}^{3}}x \right)}{\sqrt{x}}\frac{1}{\sqrt[4]{1+\frac{1}{{{x}^{2}}}}}=0} \displaystyle{\underset{x\to +\infty }{\mathop{\lim }}\,\frac{sin\left( l{{n}^{3}}x \right)}{\sqrt[4]{{{x}^{2}}+1}}=\underset{x\to +\infty }{\mathop{\lim }}\,\frac{sin\left( l{{n}^{3}}x \right)}{\sqrt{x}}\frac{\sqrt{x}}{\sqrt{x}\sqrt[4]{1+\frac{1}{{{x}^{2}}}}}=\underset{x\to +\infty }{\mathop{\lim }}\,\frac{sin\left( l{{n}^{3}}x \right)}{\sqrt{x}}\frac{1}{\sqrt[4]{1+\frac{1}{{{x}^{2}}}}}=0}](/forum/ext/geomar/texintegr/latexrender/pictures/b35785a4365bb1dd1f452050e039a61f.png)
![\displaystyle{\underset{x\to +\infty }{\mathop{\lim }}\,\frac{1}{\sqrt[4]{1+\frac{1}{{{x}^{2}}}}}=1\,\,\text{ }\!\!\kappa\!\!\text{ }\!\!\alpha\!\!\text{ }\!\!\iota\!\!\text{ }\left| \frac{sin\left( l{{n}^{3}}x \right)}{\sqrt{x}} \right|\le \frac{1}{\sqrt{x}}\Rightarrow \underset{x\to +\infty }{\mathop{\lim }}\,\frac{sin\left( l{{n}^{3}}x \right)}{\sqrt{x}}=0} \displaystyle{\underset{x\to +\infty }{\mathop{\lim }}\,\frac{1}{\sqrt[4]{1+\frac{1}{{{x}^{2}}}}}=1\,\,\text{ }\!\!\kappa\!\!\text{ }\!\!\alpha\!\!\text{ }\!\!\iota\!\!\text{ }\left| \frac{sin\left( l{{n}^{3}}x \right)}{\sqrt{x}} \right|\le \frac{1}{\sqrt{x}}\Rightarrow \underset{x\to +\infty }{\mathop{\lim }}\,\frac{sin\left( l{{n}^{3}}x \right)}{\sqrt{x}}=0}](/forum/ext/geomar/texintegr/latexrender/pictures/2ddbcd33bc716783da987f93e81d00b6.png) (από κριτήριο παρεμβολής )
(από κριτήριο παρεμβολής )





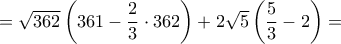
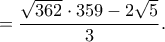
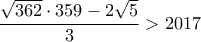


 το οποίο προφανώς ισχύει.
το οποίο προφανώς ισχύει.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 9 επισκέπτες