 .
.1) Nα μελετηθεί ως προς την μονοτονία και να βρεθεί το σύνολο τιμών της
2) Να δειχθεί οτι αντιστρέφεται και να βρεθούν τα κοινα σημεία των

3) Nα λυθεί η εξίσωση
 για να είναι σωστή η διερεύνηση
για να είναι σωστή η διερεύνηση4)

5)
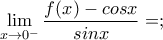
Συντονιστής: Μπάμπης Στεργίου
 .
.
 για να είναι σωστή η διερεύνηση
για να είναι σωστή η διερεύνηση
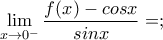
erxmer έγραψε:Δίνεται η συνάρτηση.
1) Nα μελετηθεί ως προς την μονοτονία και να βρεθεί το σύνολο τιμών της
2) Να δειχθεί οτι αντιστρέφεται και να βρεθούν τα κοινα σημεία των
3) Nα λυθεί η εξίσωση
4)
5)
 είναι παραγωγίσιμη στο
είναι παραγωγίσιμη στο  (… πράξεις με παραγωγίσιμες) με
(… πράξεις με παραγωγίσιμες) με 
 (μεμωνομένο σημείο), άρα
(μεμωνομένο σημείο), άρα  γνησίως αύξουσα στο
γνησίως αύξουσα στο 
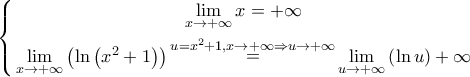
 και
και![\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to - \infty } \left[ {\ln \left( {{x^2} + 1} \right) + x} \right] = \mathop {\lim }\limits_{x \to - \infty } \left[ {x\left( {\dfrac{{\ln \left( {{x^2} + 1} \right)}}{x} + 1} \right)} \right] \mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = \mathop {\lim }\limits_{x \to - \infty } \left[ {\ln \left( {{x^2} + 1} \right) + x} \right] = \mathop {\lim }\limits_{x \to - \infty } \left[ {x\left( {\dfrac{{\ln \left( {{x^2} + 1} \right)}}{x} + 1} \right)} \right]](/forum/ext/geomar/texintegr/latexrender/pictures/03d6584644b3689d0b17e129b7314a08.png)



 είναι γνησίως αύξουσα (άρα και «1-1») θα είναι αντιστρέψιμη και επειδή είναι γνησίως αύξουσα (γνωστή πρόταση) θα είναι
είναι γνησίως αύξουσα (άρα και «1-1») θα είναι αντιστρέψιμη και επειδή είναι γνησίως αύξουσα (γνωστή πρόταση) θα είναι 
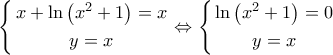

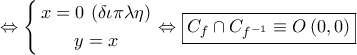 (υπάρχει επαφή των γραφικών τους παραστάσεων λόγω του διπλού σημείου).
(υπάρχει επαφή των γραφικών τους παραστάσεων λόγω του διπλού σημείου). και το γεγονός ότι η
και το γεγονός ότι η  είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο  θα ισχύει:
θα ισχύει: 
 είναι αδύνατη στο διάστημα
είναι αδύνατη στο διάστημα ![\left( -\infty ,0 \right] \left( -\infty ,0 \right]](/forum/ext/geomar/texintegr/latexrender/pictures/329daed122ff24d7ddd7cf72d5d45b16.png)
 .
.
 μοναδικό ώστε
μοναδικό ώστε  και άρα η ζητούμενη εξίσωση έχει μοναδική ρίζα.
και άρα η ζητούμενη εξίσωση έχει μοναδική ρίζα. είναι
είναι  γνησίως φθίνουσα
γνησίως φθίνουσα η οποία είναι γνησίως αύξουσα στο
η οποία είναι γνησίως αύξουσα στο  (άθροισμα γνησίως αυξουσών) και λόγω της συνέχειάς της στο
(άθροισμα γνησίως αυξουσών) και λόγω της συνέχειάς της στο 
 και
και 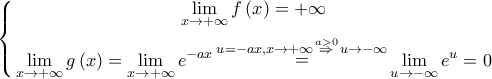
 .
.
 είναι γνησίως αύξουσα στο
είναι γνησίως αύξουσα στο  και συνεπώς η εξίσωση έχει μοναδική ρίζα.
και συνεπώς η εξίσωση έχει μοναδική ρίζα. η εξίσωση μπορεί να είναι αδύνατη ή να έχει μία λύση (διπλή) ή το πολύ δύο αλλά εδώ λογιστικά
η εξίσωση μπορεί να είναι αδύνατη ή να έχει μία λύση (διπλή) ή το πολύ δύο αλλά εδώ λογιστικά 

![\int\limits_{ - 1}^1 {\left( {x + \ln \left( {{x^2} + 1} \right)} \right)dx} = \left[ {\dfrac{{{x^2}}}{2}} \right]_{ - 1}^1 + \left[ {x\ln \left( {{x^2} + 1} \right)} \right]_{ - 1}^1 \int\limits_{ - 1}^1 {\left( {x + \ln \left( {{x^2} + 1} \right)} \right)dx} = \left[ {\dfrac{{{x^2}}}{2}} \right]_{ - 1}^1 + \left[ {x\ln \left( {{x^2} + 1} \right)} \right]_{ - 1}^1](/forum/ext/geomar/texintegr/latexrender/pictures/9b5b1dc262f55567c14f8dac1df8b52a.png)
![- \int\limits_{ - 1}^1 {\dfrac{{2{x^2}}}{{{x^2} + 1}}dx} = 2\ln 2 - \left[ {2x - 2\dfrac{{{x^3}}}{3}} \right]_{ - 1}^1 = 2\ln 2 \leqslant 2 + 2\ln 2 - \int\limits_{ - 1}^1 {\dfrac{{2{x^2}}}{{{x^2} + 1}}dx} = 2\ln 2 - \left[ {2x - 2\dfrac{{{x^3}}}{3}} \right]_{ - 1}^1 = 2\ln 2 \leqslant 2 + 2\ln 2](/forum/ext/geomar/texintegr/latexrender/pictures/8cf89074b321d6337b2d2f7133f661cb.png) .
.


 από
από  ως
ως  δε κάνει
δε κάνει  .... οπότε πρέπει να ξανά δεις το ερώτημα αυτό .
.... οπότε πρέπει να ξανά δεις το ερώτημα αυτό .

![x\in [-1,1]\Rightarrow ln(x^{2}+1)\leq ln2 x\in [-1,1]\Rightarrow ln(x^{2}+1)\leq ln2](/forum/ext/geomar/texintegr/latexrender/pictures/601e1b6b5dcc3a2de4fe72184ae99e29.png)
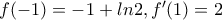

 μπροστά.
μπροστά.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 7 επισκέπτες